http://www.kdnuggets.com/2016/08/10-algorithms-machine-learning-engineers.html/2
It is no
doubt that the sub-field of machine learning / artificial intelligence
has increasingly gained more popularity in the past couple of years. As
Big Data is the hottest trend in the tech industry at the moment,
machine learning is incredibly powerful to make predictions or
calculated suggestions based on large amounts of data. Some of the most
common examples of machine learning are Netflix’s algorithms to make
movie suggestions based on movies you have watched in the past or
Amazon’s algorithms that recommend books based on books you have bought
before.
So
if you want to learn more about machine learning, how do you start? For
me, my first introduction is when I took an Artificial Intelligence
class when I was studying abroad in Copenhagen. My lecturer is a
full-time Applied Math and CS professor at the Technical University of
Denmark, in which his research areas are logic and artificial, focusing
primarily on the use of logic to model human-like planning, reasoning
and problem solving. The class was a mix of discussion of theory/core
concepts and hands-on problem solving. The textbook that we used is one
of the AI classics: Peter Norvig’s Artificial Intelligence — A Modern Approach,
in which we covered major topics including intelligent agents,
problem-solving by searching, adversarial search, probability theory,
multi-agent systems, social AI, philosophy/ethics/future of AI. At the
end of the class, in a team of 3, we implemented simple search-based
agents solving transportation tasks in a virtual environment as a
programming project.
I
have learned a tremendous amount of knowledge thanks to that class, and
decided to keep learning about this specialized topic. In the last few
weeks, I have been multiple tech talks in San Francisco on deep
learning, neural networks, data architecture — and a Machine Learning
conference with a lot of well-known professionals in the field. Most
importantly, I enrolled in Udacity’s Intro to Machine Learning online
course in the beginning of June and has just finished it a few days
ago. In this post, I want to share some of the most common machine
learning algorithms that I learned from the course.
Machine
learning algorithms can be divided into 3 broad categories — supervised
learning, unsupervised learning, and reinforcement learning. Supervised learning is useful in cases where a property (label) is available for a certain dataset (training set), but is missing and needs to be predicted for other instances. Unsupervised learning is useful in cases where the challenge is to discover implicit relationships in a given unlabeled dataset (items are not pre-assigned). Reinforcement learning
falls between these 2 extremes — there is some form of feedback
available for each predictive step or action, but no precise label or
error message. Since this is an intro class, I didn’t learn about
reinforcement learning, but I hope that 10 algorithms on supervised and
unsupervised learning will be enough to keep you interested.
Supervised Learning
1. Decision Trees: A
decision tree is a decision support tool that uses a tree-like graph or
model of decisions and their possible consequences, including
chance-event outcomes, resource costs, and utility. Take a look at the
image to get a sense of how it looks like.
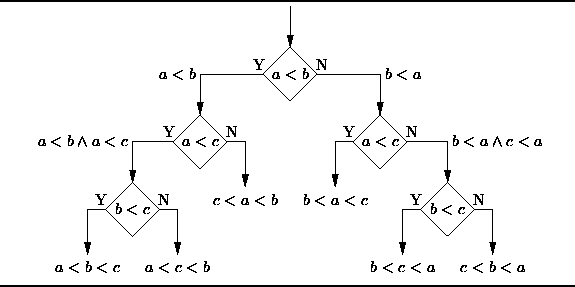
From
a business decision point of view, a decision tree is the minimum
number of yes/no questions that one has to ask, to assess the
probability of making a correct decision, most of the time. As a method,
it allows you to approach the problem in a structured and systematic
way to arrive at a logical conclusion.
2. Naïve Bayes Classification: Naïve
Bayes classifiers are a family of simple probabilistic classifiers
based on applying Bayes’ theorem with strong (naïve) independence
assumptions between the features. The featured image is the
equation — with P(A|B) is posterior probability, P(B|A) is likelihood,
P(A) is class prior probability, and P(B) is predictor prior
probability.
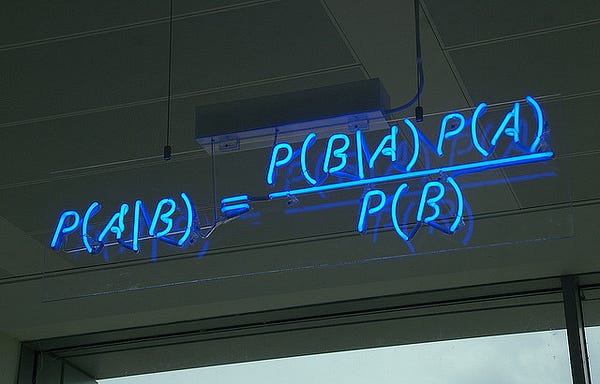
Some of real world examples are:
· To mark an email as spam or not spam
· Classify a news article about technology, politics, or sports
· Check a piece of text expressing positive emotions, or negative emotions?
· Used for face recognition software.
3. Ordinary Least Squares Regression: If
you know statistics, you probably have heard of linear regression
before. Least squares is a method for performing linear regression. You
can think of linear regression as the task of fitting a straight line
through a set of points. There are multiple possible strategies to do
this, and “ordinary least squares” strategy go like this — You can draw a
line, and then for each of the data points, measure the vertical
distance between the point and the line, and add these up; the fitted
line would be the one where this sum of distances is as small as
possible.
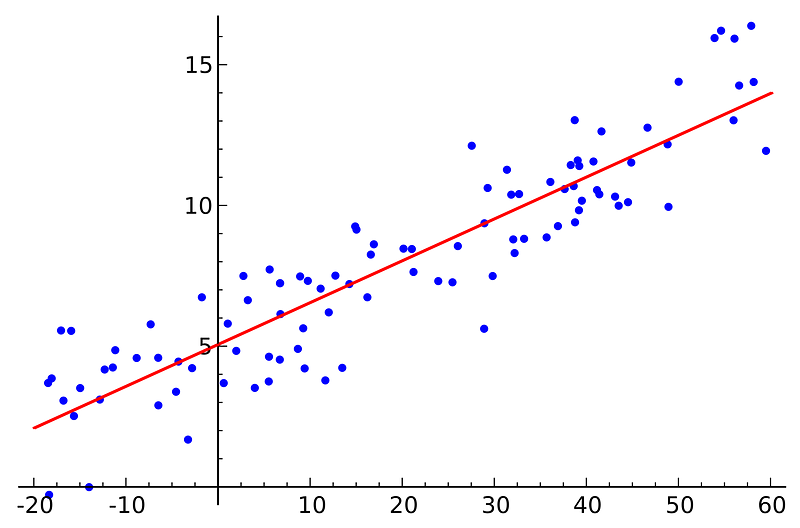
Linear
refers the kind of model you are using to fit the data, while least
squares refers to the kind of error metric you are minimizing over.
4. Logistic Regression: Logistic
regression is a powerful statistical way of modeling a binomial outcome
with one or more explanatory variables. It measures the relationship
between the categorical dependent variable and one or more independent
variables by estimating probabilities using a logistic function, which
is the cumulative logistic distribution.
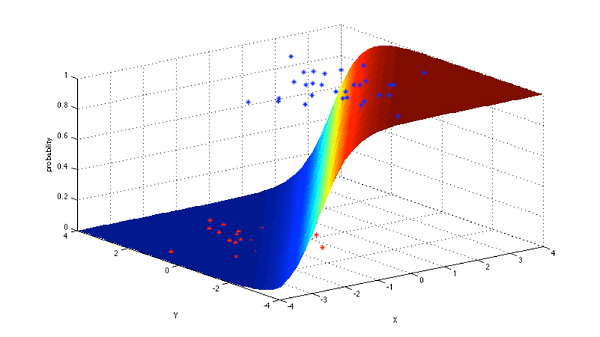
In general, regressions can be used in real-world applications such as:
· Credit Scoring
· Measuring the success rates of marketing campaigns
· Predicting the revenues of a certain product
· Is there going to be an earthquake on a particular day?
5. Support Vector Machines: SVM
is binary classification algorithm. Given a set of points of 2 types in
N dimensional place, SVM generates a (N — 1) dimensional hyperlane to
separate those points into 2 groups. Say you have some points of 2 types
in a paper which are linearly separable. SVM will find a straight line
which separates those points into 2 types and situated as far as
possible from all those points.
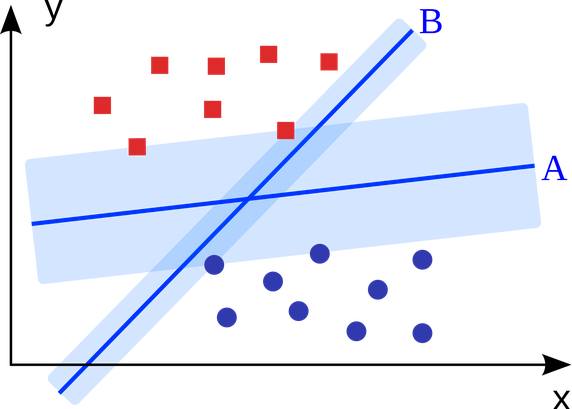
In
terms of scale, some of the biggest problems that have been solved
using SVMs (with suitably modified implementations) are display
advertising, human splice site recognition, image-based gender
detection, large-scale image classification…
6. Ensemble Methods: Ensemble
methods are learning algorithms that construct a set of classifiers and
then classify new data points by taking a weighted vote of their
predictions. The original ensemble method is Bayesian averaging, but
more recent algorithms include error-correcting output coding, bagging,
and boosting.
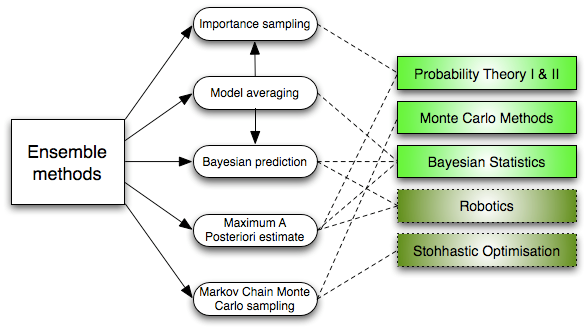
So how do ensemble methods work and why are they superior to individual models?
· They average out biases:
If you average a bunch of democratic-leaning polls and
republican-leaning polls together, you will get an average something
that isn’t leaning either way.
· They reduce the variance:
The aggregate opinion of a bunch of models is less noisy than the
single opinion of one of the models. In finance, this is called
diversification — a mixed portfolio of many stocks will be much less
variable than just one of the stocks alone. This is why your models will
be better with more data points rather than fewer.
· They are unlikely to over-fit: If
you have individual models that didn’t over-fit, and you are combining
the predictions from each model in a simple way (average, weighted
average, logistic regression), then there’s no room for over-fitting.
Unsupervised Learning
7. Clustering Algorithms: Clustering is the task of grouping a set of objects such that objects in the same group (cluster) are more similar to each other than to those in other groups.
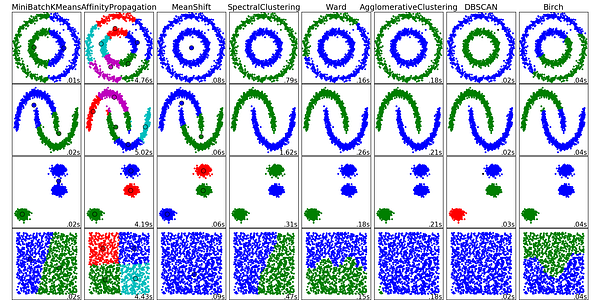
Every clustering algorithm is different, and here are a couple of them:
· Centroid-based algorithms
· Connectivity-based algorithms
· Density-based algorithms
· Probabilistic
· Dimensionality Reduction
· Neural networks / Deep Learning
8. Principal Component Analysis: PCA
is a statistical procedure that uses an orthogonal transformation to
convert a set of observations of possibly correlated variables into a
set of values of linearly uncorrelated variables called principal
components.
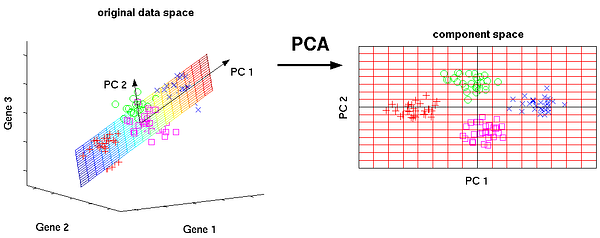
Some
of the applications of PCA include compression, simplifying data for
easier learning, visualization. Notice that domain knowledge is very
important while choosing whether to go forward with PCA or not. It is
not suitable in cases where data is noisy (all the components of PCA
have quite a high variance).
9. Singular Value Decomposition: In linear algebra, SVD is a factorization of a real complex matrix. For a given m * n matrix M, there exists a decomposition such that M = UΣV, where U and V are unitary matrices and Σ is a diagonal matrix.
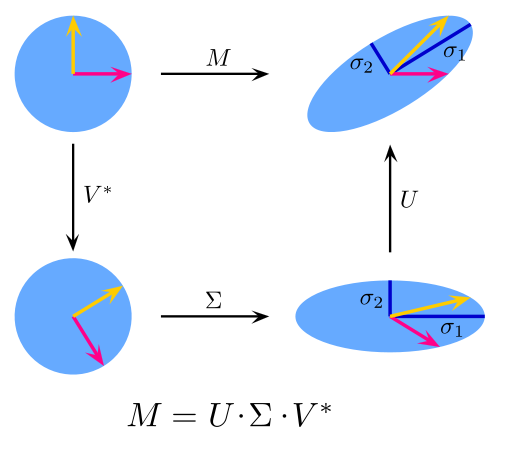
PCA
is actually a simple application of SVD. In computer vision, the 1st
face recognition algorithms used PCA and SVD in order to represent faces
as a linear combination of “eigenfaces”, do dimensionality reduction,
and then match faces to identities via simple methods; although modern
methods are much more sophisticated, many still depend on similar
techniques.
10. Independent Component Analysis: ICA
is a statistical technique for revealing hidden factors that underlie
sets of random variables, measurements, or signals. ICA defines a
generative model for the observed multivariate data, which is typically
given as a large database of samples. In the model, the data variables
are assumed to be linear mixtures of some unknown latent variables, and
the mixing system is also unknown. The latent variables are assumed
non-gaussian and mutually independent, and they are called independent
components of the observed data.
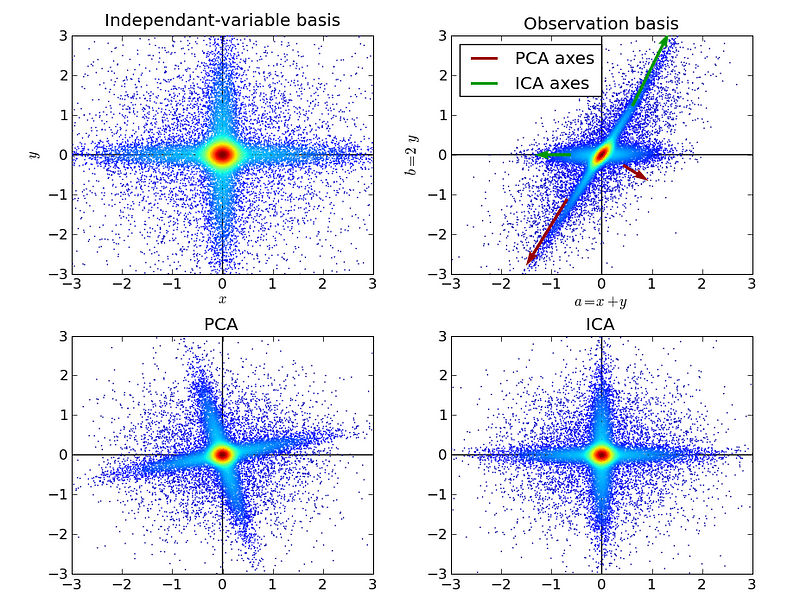
ICA
is related to PCA, but it is a much more powerful technique that is
capable of finding the underlying factors of sources when these classic
methods fail completely. Its applications include digital images,
document databases, economic indicators and psychometric measurements.
Now
go forth and wield your understanding of algorithms to create machine
learning applications that make better experiences for people
everywhere.
No comments:
Post a Comment