I
have always worked on computer vision applications. Honestly,
transformers and attention-based methods were always the fancy things
that I never spent the time to study. You know, maybe later and etc. Now
they managed to reach state-of-the-art performance in ImageNet [3].
In
NLP, transformers and attention have been utilized successfully in a
plethora of tasks including reading comprehension, abstractive
summarization, word completion, and others.
After a lot of reading and searching, I realized that it is crucial to understand how attention emerged from NLP and machine translation.
This is what this article is all about. After this article, we will
inspect the transformer model like a boss. I give you my word.
Let’s start from the beginning: What is attention? Glad you asked!
Memory is attention through time. ~ Alex Graves 2020 [1]
Always keep this in the back of your mind.
The attention mechanism emerged naturally from problems that deal with time-varying data (sequences).
So, since we are dealing with “sequences”, let’s formulate the problem
in terms of machine learning first. Attention became popular in the
general task of dealing with sequences.
Sequence to sequence learning
Before attention and transformers, Sequence to Sequence (Seq2Seq) worked pretty much like this:

The elements of the sequence x1,x2, etc. are usually called tokens. They can be literally anything. For instance, text representations, pixels, or even images in the case of videos.
OK. So why do we use such models?
The goal is to transform an input sequence (source) to a new one (target).
The two sequences can be of the same or arbitrary length.
In case you are wondering, recurrent neural networks (RNNs) dominated this category of tasks. The reason is simple: we liked to treat sequences sequentially. Sounds obvious and optimal? Transformers proved us it’s not!
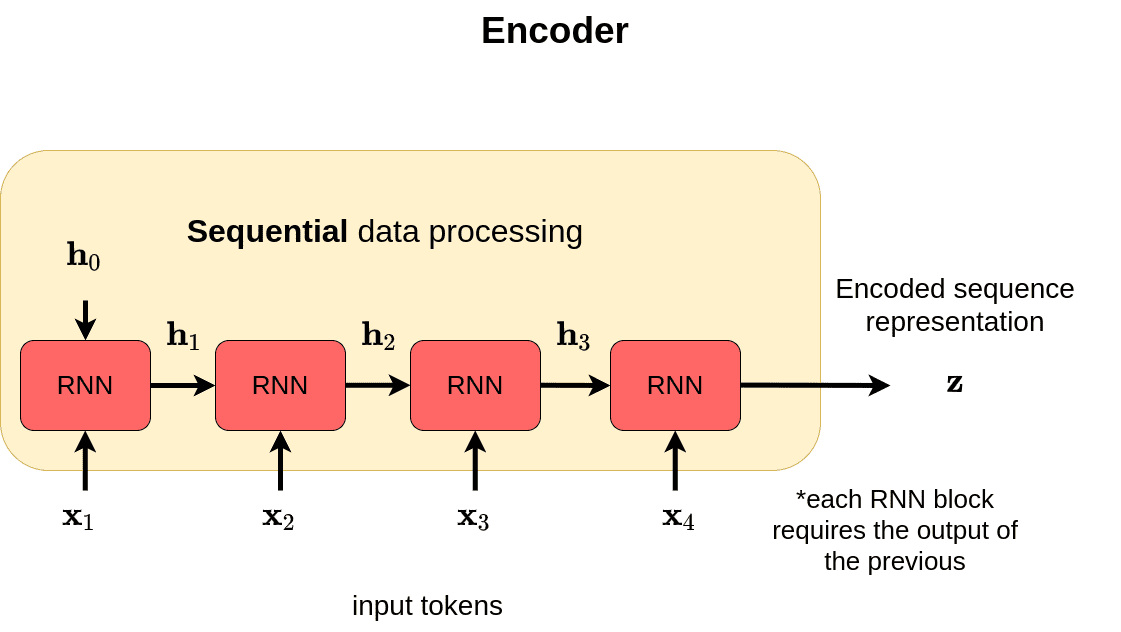
A high-level view of encoder and decoder
The encoder and decoder are nothing more than stacked RNN layers, such as LSTM’s. The encoder processes the input and produces one compact representation, called z, from all the input timesteps. It can be regarded as a compressed format of the input.
On the other hand, the decoder receives the context vector z
and generates the output sequence. The most common application of
Seq2seq is language translation. We can think of the input sequence as
the representation of a sentence in English and the output as the same
sentence in French.
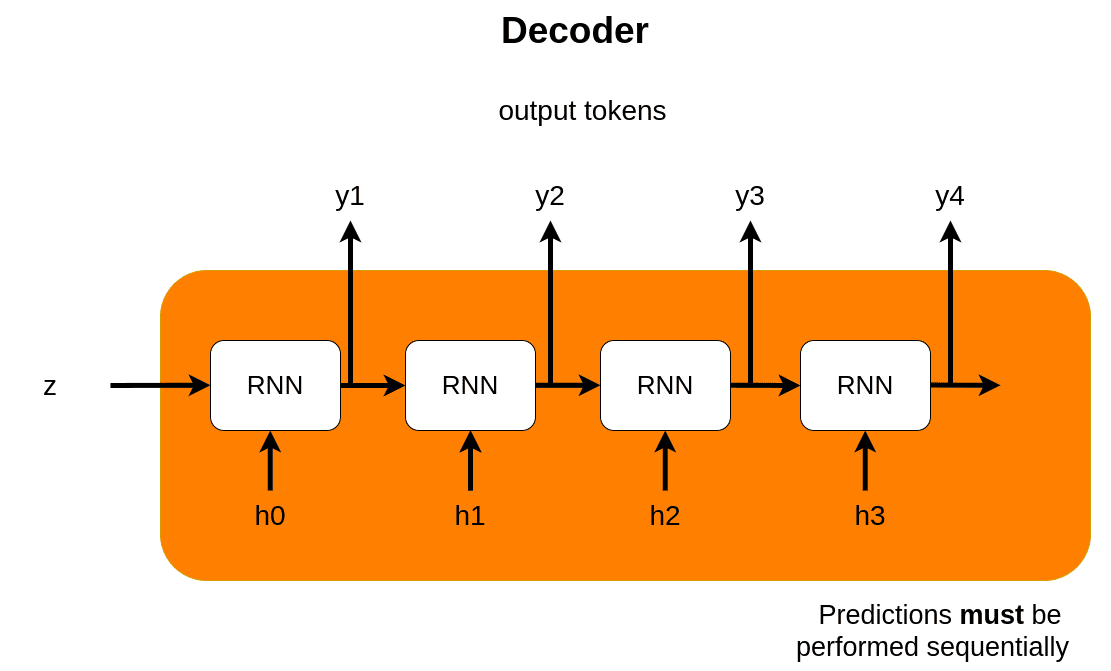
In fact, RNN-based architectures used to work very well especially with LSTM and GRU components.
The problem? Only for small sequences (<20 timesteps). Visually:
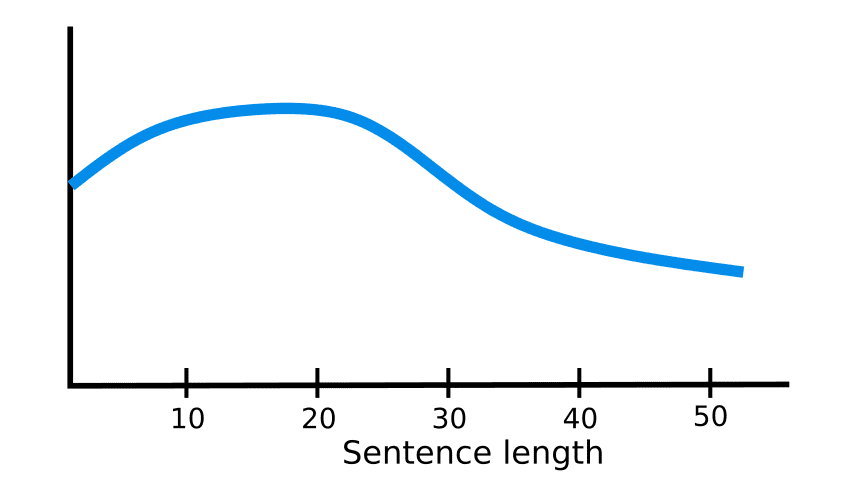
Let’s inspect some of the reasons why this holds true.
The limitations of RNN’s
The intermediate representation z cannot encode information from all the input timesteps. This is commonly known as the bottleneck problem. The vector z needs to capture all the information about the source sentence.
In
theory, mathematics indicate that this is possible. However in
practice, how far we can see in the past (the so-called reference
window) is finite. RNN’s tend to forget information from timesteps that are far behind.
Let’s see a concrete example. Imagine a sentence of 97 words:
“On offering to help the blind man, the man who then stole his car,
had not, at that precise moment, had any evil intention, quite the
contrary, what he did was nothing more than obey those feelings of
generosity and altruism which, as everyone knows, are the two best
traits of human nature and to be found in much more hardened criminals
than this one, a simple car-thief without any hope of
advancing in his profession, exploited by the real owners of this
enterprise, for it is they who take advantage of the needs of the poor.” ~ Jose Saramago, “Blindness.”
Notice anything wrong? Hmmm… The bold words that facilitate the understanding are quite far!
In most cases, the vector z will be unable to compress the information of the early words as well as the 97th word.
Eventually,
the system pays more attention to the last parts of the sequence.
However, this is not usually the optimal way to approach a sequence task
and it is not compatible with the way humans translate or even
understand language.
Furthermore, the stacked RNN layer usually create the well-know vanishing gradient problem, as perfectly visualized in the distill article on RNN’s:
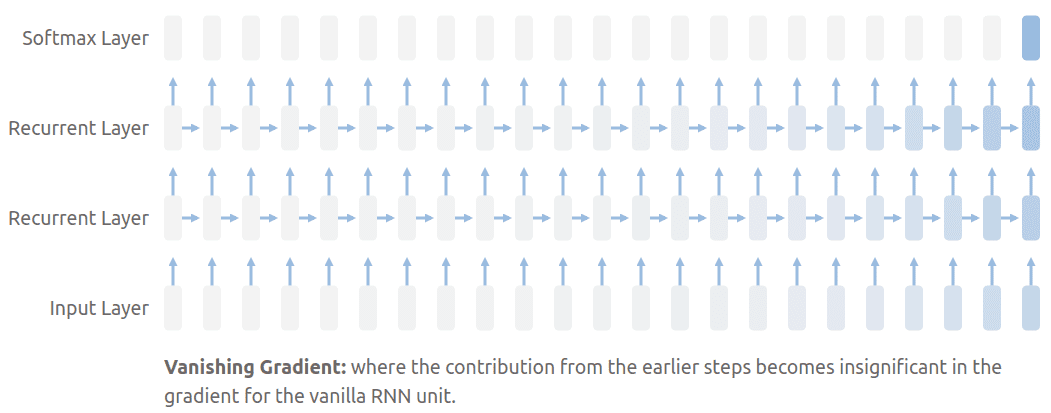 The stacked layers in RNN's may result in the vanishing gradient problem. Source
The stacked layers in RNN's may result in the vanishing gradient problem. Source
Thus, let us move beyond the standard encoder-decoder RNN.
Attention to the rescue!
Attention was born in order to address these two things on the Seq2seq model. But how?
The core idea is that the context vector z should have access to all parts of the input sequence instead of just the last one.
In other words, we need to form a direct connection with each timestamp.
This idea was originally proposed for computer vision. Larochelle and Hinton [5]
proposed that by looking at different parts of the image (glimpses), we
can learn to accumulate information about a shape and classify the
image accordingly.
The same principle was later extended to
sequences. We can look at all the different words at the same time and
learn to “pay attention“ to the correct ones depending on the task at
hand.
And behold. This is what we now call attention, which is simply a notion of memory, gained from attending at multiple inputs through time.
It
is crucial in my humble opinion to understand the generality of this
concept. To this end, we will cover all the different types that one can
divide attention mechanisms.
Types of attention: implicit VS explicit
Before we continue with a concrete example of how attention is used on machine translation, let’s clarify one thing:
Very deep neural networks already learn a form of implicit attention [6].
Deep networks are very rich function approximators. So, without any further modification, they tend to ignore parts of the input and focus on others.
For instance, when working on human pose estimation, the network will
be more sensitive to the pixels of the human body. Here is an example of
self-supervised approaches to videos:

Where activations tend to focus when trained in a self-supervised way. Image from Misra et al. ECCV 2016. Source
“Many activation units show a preference for human body parts and pose.” ~ Misra et al. 2016
One
way to visualize implicit attention is by looking at the partial
derivatives with respect to the input. In math, this is the Jacobian matrix, but it’s out of the scope of this article.
However,
we have many reasons to enforce this idea of implicit attention.
Attention is quite intuitive and interpretable to the human mind. Thus,
by asking the network to ‘weigh’ its sensitivity to the input based on memory from previous inputs, we introduce explicit attention. From now on, we will refer to this as attention.
Types of attention: hard VS soft
Another
distinction we tend to make is between hard and soft attention. In all
the previous cases, we refer to attention that is parametrized by differentiable functions. For the record, this is termed as soft attention in the literature. Officially:
Soft attention means that the function varies smoothly over its domain and, as a result, it is differentiable.
Historically, we had another concept called hard attention.
An intuitive example: You can imagine a robot in a labyrinth that has to make a hard decision on which path to take, as indicated by the red dots.
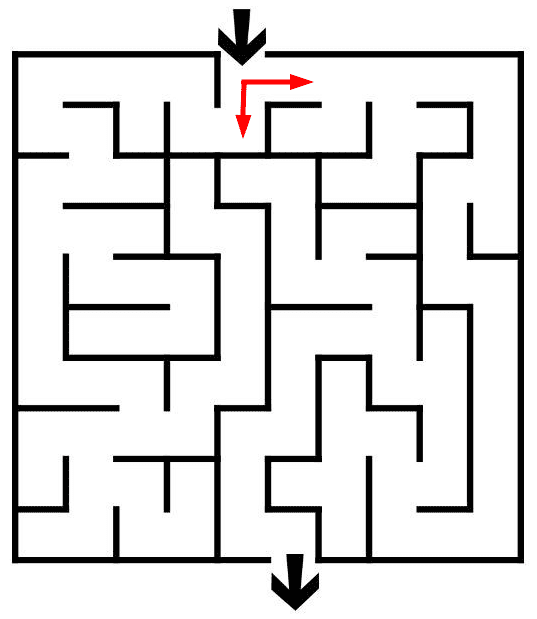 A decision in the labyrinth. Source
A decision in the labyrinth. Source
In general, hard means that it can be described by discrete variables while soft attention is described by continuous variables. In other words, hard attention replaces a deterministic method with a stochastic sampling model.
In
the next example, starting from a random location in the image tries to
find the “important pixels” for classification. Roughly, the algorithm
has to choose a direction to go inside the image, during training.
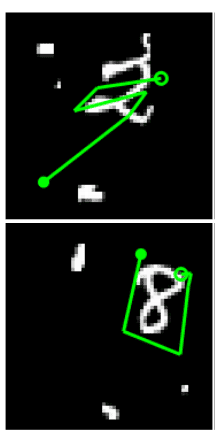 An example of hard attention.Source
An example of hard attention.Source
Since
hard attention is non-differentiable, we can’t use the standard
gradient descent. That’s why we need to train them using Reinforcement
Learning (RL) techniques such as policy gradients and the REINFORCE algorithm [6].
Nevertheless,
the major issue with the REINFORCE algorithm and similar RL methods is
that they have a high variance. To summarize:
Hard attention
can be regarded as a switch mechanism to determine whether to attend to
a region or not, which means that the function has many abrupt changes
over its domain.
Ultimately, given that we already have all the sequence tokens available, we can relax the definition of hard
attention. In this way, we have a smooth differentiable function that
we can train end to end with our favorite backpropagation.
Let’s get back to our showcase to see it in action!
Attention in our encoder-decoder example
In the encoder-decoder RNN case, given previous state in the decoder as yi−1 and the the hidden state h=h1,h2,hn, we have something like this:
ei=attentionnet(yi−1,h)∈RnThe
index i indicates the prediction step. Essentially, we define a score
between the hidden state of the decoder and all the hidden states of the
encoder.
More specifically, for each hidden state (denoted by j) h1,h2,hn we will calculate a scalar:
eij=attentionnet(yi−1,hj)Visually, in our beloved example, we have something like this:
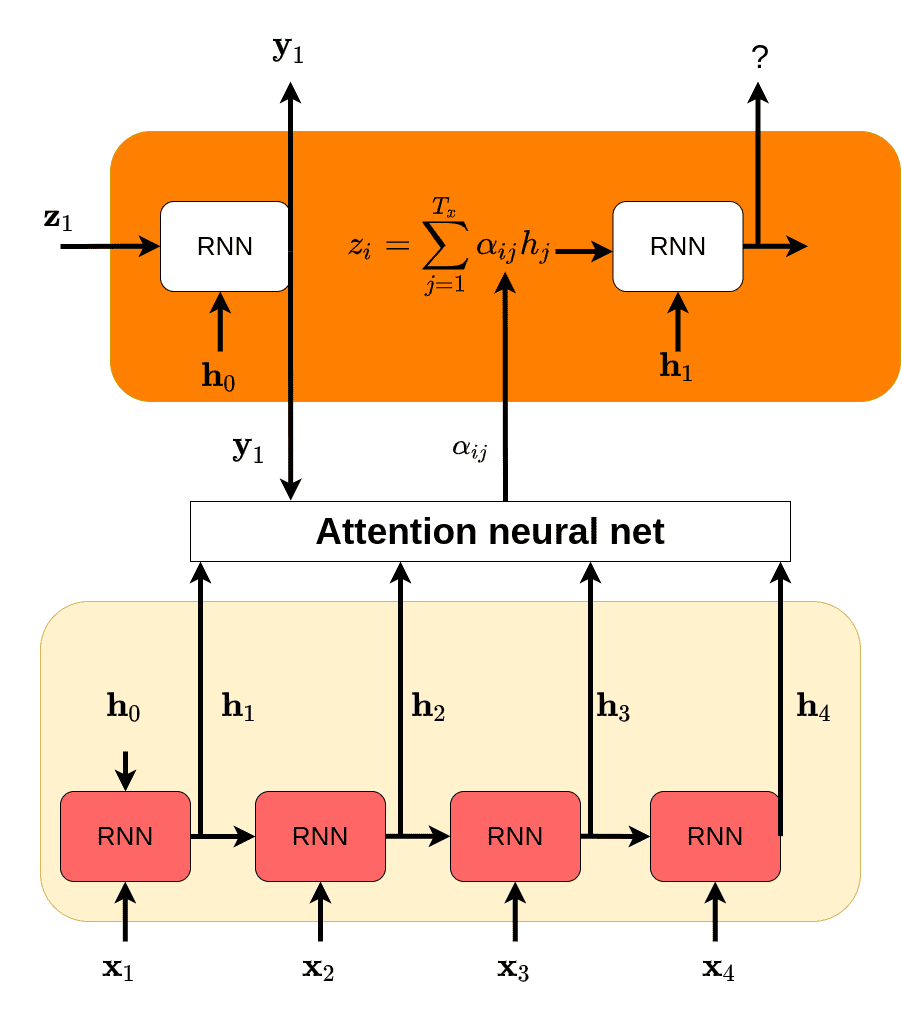
Notice anything strange?
I used the symbol e in the equation and α in the diagram! Why?
Because, we want some extra properties: a) to make it a probability distribution
and b) to make the scores to be far from each other. The latter results
in having more confident predictions and is nothing more than our well
known softmax.
αij=∑k=1Txexp(eik)exp(eij)Finally, here is where the new magic will happen:
zi=j=1∑TαijhjIn theory, attention is defined as the weighted average of values. But this time, the weighting is a learned function! Intuitively, we can think of αij as data-dependent dynamic weights. Therefore, it is obvious that we need a notion of memory, and as we said attention weight store the memory that is gained through time
All the aforementioned are independent of how we choose to model attention! We will get down to that in a bit.
Attention as a trainable weight mean for machine translation
I find that the most intuitive way to understand attention in NLP tasks is to think of it as a (soft) alignment between words. But what does this alignment look like? Excellent question!
In machine translation, we can visualize the attention of a trained network using a heatmap such as below. Note that scores are computed dynamically.
 Image by Neural Machine translation paper. Source
Image by Neural Machine translation paper. Source
Notice what happens in the active non-diagonal elements. In the marked red area, the model learned to swap the order of words in translation. Also note that this is not a 1-1 relationship but a 1 to many, meaning that an output word is affected by more than one input word (each one with different importance).
How do we compute attention?
In our previous encoder-decoder example, we denoted attention as attentionnet(yi−1,h) which indicates that it’s the output of a small neural network with inputs the previous state of the decoder as yi−1 and the hidden state h=h1,h2,hn. In fact all we need is a score that describes the relationship between the two states and captures how “aligned” they are.
While
a small neural network is the most prominent approach, over the years
there have been many different ideas to compute that score. The simplest
one, as shown in Luong [7], computes attention as the dot product between the two states yi−1h. Extending this idea we can introduce a trainable weight matrix in between yi−1Wah, where Wa
is an intermediate wmatrix with learnable weights. Extending even
further, we can also include an activation function in the mix which
leads to our familiar neural network approach vaTtanh(Wa[h;yi−1]) proposed by Bahdanau [2]
In certain cases, the alignment is only affected by the position of the hidden state, which can be formulated using simply a softmax function softmax(yi−1,h)
The last one worth mentioning can be found in Graves A. [8] in the context of Neural Turing Machines and calculates attention as a cosine similarity cosine[yi−1,h]
To summarize the different techniques, I’ll borrow this table from Lillian Weng’s excellent article. The symbol st denotes the predictions (I used yt), while different W indicate trainable matrices:
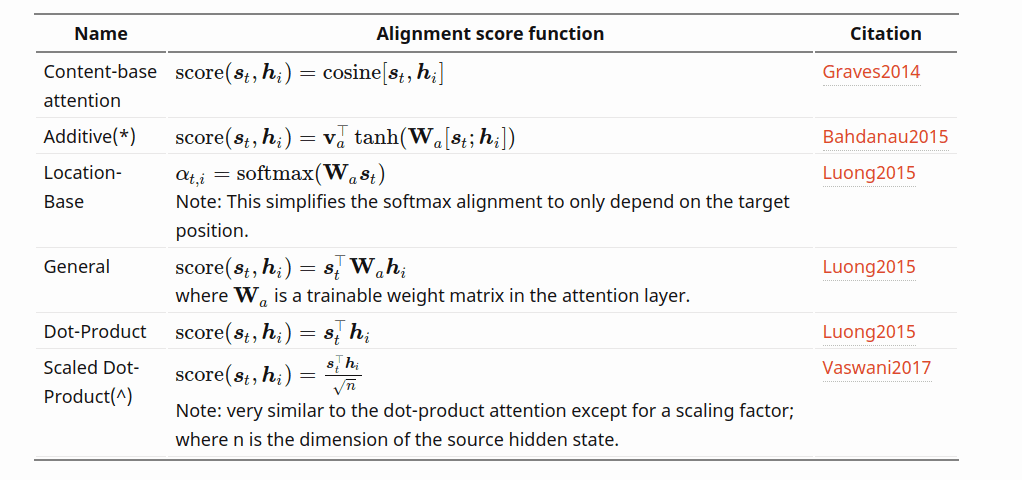 Ways to compute attention. Source
Ways to compute attention. Source
The approach that stood the test of time, however, is the last one proposed by Bahdanau et al. [2]: They parametrize attention as a small fully connected neural network. And obviously, we can extend that to use more layers.
This
effectively means that attention is now a set of trainable weights that
can be tuned using our standard backpropagation algorithm.
As perfectly stated by Bahdanau et al. [2]:
“Intuitively,
this implements a mechanism of attention in the decoder. The decoder
decides parts of the source sentence to pay attention to. By letting the
decoder have an attention mechanism, we relieve the encoder from the burden of having to encode all information in the source sentence into a fixed-length vector.
With this new approach, the information can be spread throughout the
sequence of annotations, which can be selectively retrieved by the
decoder accordingly.” ~ Neural machine translation by jointly learning to align and translate
So, what do we lose? Hmm... I am glad you asked!
We sacrificed computational complexity. We have another neural network to train and we need to have O(T2) weights (where T is the length of both the input and output sentence).
Quadratic complexity can often be a problem! Unless you own Google ;)
And that brings us to local attention.
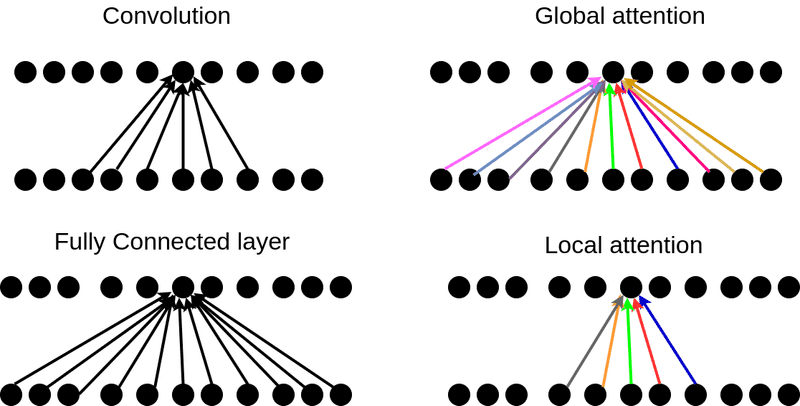
Global vs Local Attention
Until
now we assumed that attention is computed over the entire input
sequence (global attention). Despite its simplicity, it can be
computationally expensive and sometimes unnecessary. As a result, there
are papers that suggest local attention as a solution.
In local attention, we consider only a subset of the input units/tokens.
Evidently, this can sometimes be better for very long sequences. Local attention can also be merely seen as hard attention since we need to take a hard decision first, to exclude some input units.
Let’s wrap up the operations in a simple diagram:
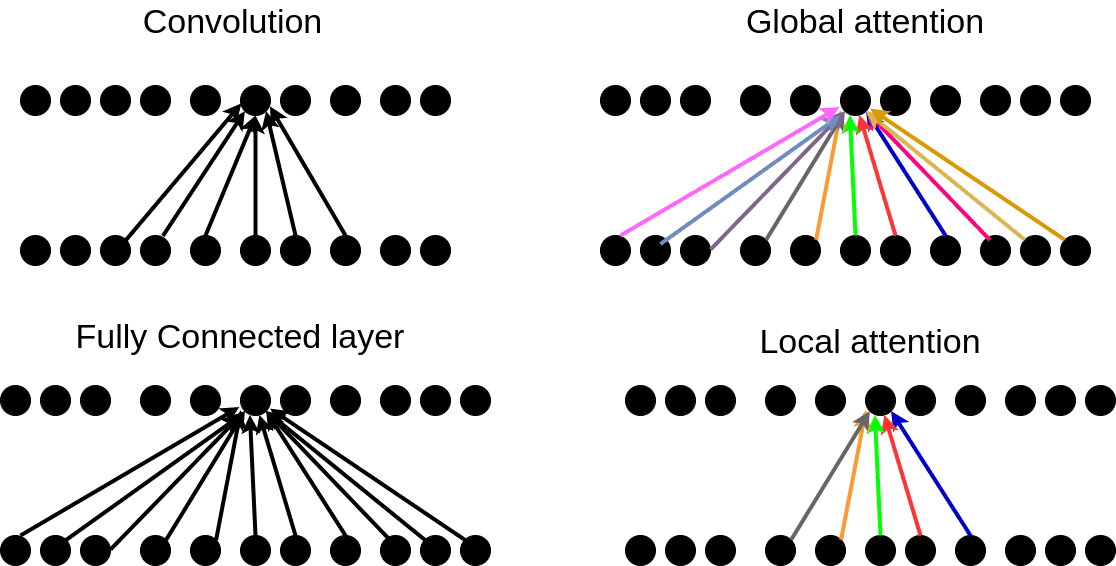
The colors in the attention indicate that
these weights are constantly changing while in convolution and fully
connected layers they are slowly changing by gradient descent.
The last and undeniably the most famous category is self-attention.
We can also define the attention of the same sequence, called self-attention. Instead of looking for an input-output sequence association/alignment, we are now looking for scores between the elements of the sequence, as depicted below:
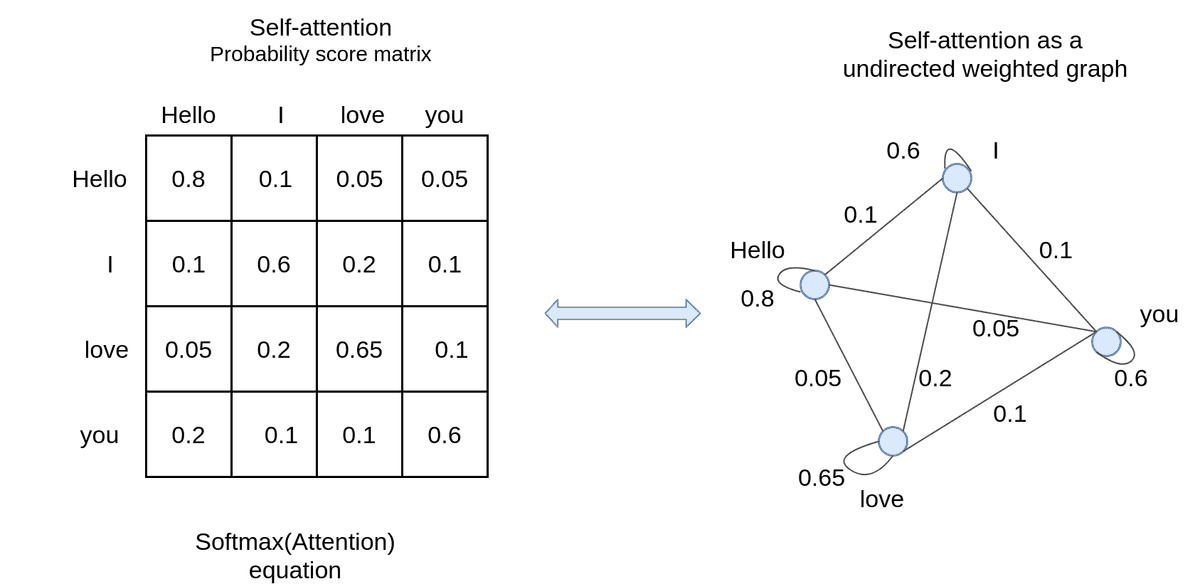
Personally, I like to think of self-attention as a
graph. Actually, it can be regarded as a (k-vertex) connected undirected
weighted graph. Undirected indicates that the matrix is symmetric.
In maths we have: self-attentionnet(x,x).
The self-attention can be computed in any mentioned trainable way. The
end goal is to create a meaningful representation of the sequence before
transforming to another.
Advantages of Attention
Admittedly,
attention has a lot of reasons to be effective apart from tackling the
bottleneck problem. First, it usually eliminates the vanishing gradient problem, as they provide direct connections between the encoder states and the decoder. Conceptually, they act similarly as skip connections in convolutional neural networks.
One other aspect that I’m personally very excited about is explainability.
By inspecting the distribution of attention weights, we can gain
insights into the behavior of the model, as well as to understand its
limitations.
Think, for example, the English-to-French heatmap we
showed before. I had an aha moment when I saw the swap of words in
translation. Don’t tell me that it isn't extremely useful.
Attention beyond language translation
Sequences are everywhere!
While transformers
are definitely used for machine translation, they are often considered
as general-purpose NLP models that are also effective on tasks like text
generation, chatbots, text classification, etc. Just take a look at
Google’s BERT or OpenAI’s GPT-3.
But we can also go beyond NLP.
We briefly saw attention being used in image classification models,
where we look at different parts of an image to solve a specific task.
In fact, visual attention models recently outperformed the state of the
art Imagenet model [3]. We also have seen examples in healthcare, recommender systems, and even on graph neural networks.
To
summarize everything said so far in a nutshell, I would say: Attention
is much more than transformers and transformers are more than NLP
approaches.
Only time will prove me right or wrong!
Conclusion
For a more holistic approach on NLP approaches with attention models we recommend the Coursera course.
So if you aim to understand transformers, now you are ready to go! This
article was about seeing through the equations of attention.
Attention
is a general mechanism that introduces the notion of memory. The memory
is stored in the attention weights through time and it gives us an
indication on where to look. Finally, we clarified all the possible
distinctions of attention and showed a couple of famous ways to compute
it.
As a next step, I would advise the TensorFlow tutorial on attention, which you can run in Google Colab.
If you want to discover in more depth the principles of attention, the
best resource is undeniably Alex Graves’ video from DeepMind:
https://www.youtube.com/watch?v=AIiwuClvH6k
If you reached this point, I guess you are super ready for our Transformer article.
Cited as:
@article{adaloglou2020normalization,
title = "How attention works in deep learning: understanding the attention mechanism in sequence models",
author = "Adaloglou, Nikolas and Karagiannakos, Sergios",
journal = "https://theaisummer.com/",
year = "2020",
url = "https://theaisummer.com/attention/"
}
Acknowledgements
Thanks to the awesome Reddit community for identifying my mistake. Memory is attention through time and not vice versa.
References
- [1] DeepMind’s deep learning videos 2020 with UCL, Lecture: Attention and Memory in Deep Learning, Alex Graves
- [2] Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
- [3][an image is worth 16x16 words: transformers for image recognition at scale](https://openreview.net/forum?id=YicbFdNTTy), Anonymous ICLR 2021 submission
- [4] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).
- [5] Larochelle H., Hinton G, (2010), Learning to combine foveal glimpses with a third-order Boltzmann machine
- [6] Mnih V., Heess N., Graves A., Kavukcuoglu K., (2014), Recurrent Models of Visual Attention
- [7] Luong M., Pham H , Manning C. D., (2015), Effective Approaches to Attention-based Neural Machine Translation
- [8] Graves A., Wayne G. ,Danihelka I., (2014), Neural turing machines
- [9] Weng L., (2018), Attention? Attention!, lilianweng.github.io/lil-log
- [10] Stanford University School of Engineering, (2017), Lecture 10: Neural Machine Translation and Models with Attention