I took a Deep Learning course through The Bradfield School of Computer Science in June. This series is a journal about what I learned in class, and what I’ve learned since.
This
is the first article in this series, and is is about the recommended
preparation for the Deep Learning course and what we learned in the
first class. Read the second article here, and the third here.
Although
normally the “prework” comes before the introduction, I’m going to give
the 30,000 foot view of the fields of artificial intelligence, machine
learning, and deep learning at the top. I have found that this context
can really help us understand why the prerequisites seem so broad, and
help us study just the essentials. Besides, the history and landscape of
artificial intelligence is interesting, so lets dive in!
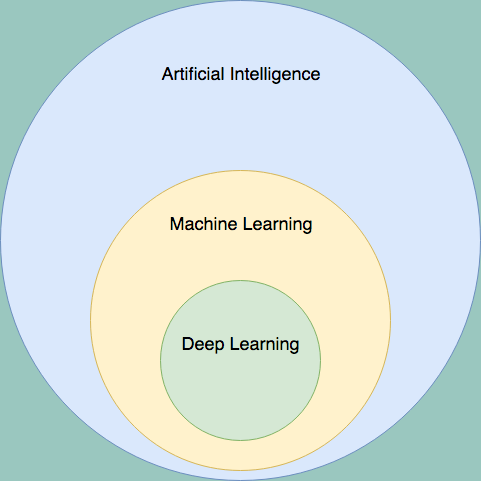
Artificial Intelligence, Machine Learning, and Deep Learning
Deep
learning is a subset of machine learning. Machine learning is a subset
of artificial intelligence. Said another way — all deep learning
algorithms are machine learning algorithms, but many machine learning
algorithms do not use deep learning. As a Venn Diagram, it looks like
this:
Deep learning refers specifically to a class of algorithm called a neural network,
and technically only to “deep” neural networks (more on that in a
second). This first neural network was invented in 1949, but back then
they weren’t very useful. In fact, from the 1970’s to the 2010’s
traditional forms of AI would consistently outperform neural network
based models.
These
non-learning types of AI include rule based algorithms (imagine an
extremely complex series of if/else blocks); heuristic based AIs such as
A* search; constraint satisfaction algorithms like Arc Consistency; tree search algorithms such as minimax (used by the famous Deep Blue chess AI); and more.
There
were two things preventing machine learning, and especially deep
learning, from being successful. Lack of availability of large datasets
and lack of availability of computational power. In 2018 we have
exabytes of data, and anyone with an AWS account and a credit card has
access to a distributed supercomputer. Because of the new availability
of data and computing power, Machine learning — and especially deep
learning — has taken the AI world by storm.
You should know that there are other categories of machine learning such as unsupervised learning and reinforcement learning but for the rest of this article, I will be talking about a subset of machine learning called supervised learning.
Supervised
learning algorithms work by forcing the machine to repeatedly make
predictions. Specifically, we ask it to make predictions about data that
we (the humans) already know the correct answer for. This is called
“labeled data” — the label is whatever we want the machine to predict.
Here’s
an example: let’s say we wanted to build an algorithm to predict if
someone will default on their mortgage. We would need a bunch of
examples of people who did and did not default on their mortgages. We
will take the relevant data about these people; feed them into the
machine learning algorithm; ask it to make a prediction about each
person; and after it guesses we tell the machine what the right answer
actually was. Based on how right or wrong it was the machine learning
algorithm changes how it makes predictions.
We repeat this process many many
times, and through the miracle of mathematics, our machine’s
predictions get better. The predictions get better relatively slowly
though, which is why we need so much data to train these algorithms.
Machine learning algorithms such as linear regression, support vector machines, and decision trees
all “learn” in different ways, but fundamentally they all apply this
same process: make a prediction, receive a correction, and adjust the
prediction mechanism based on the correction. At a high level, it’s
quite similar to how a human learns.
Recall
that deep learning is a subset of machine learning which focuses on a
specific category of machine learning algorithms called neural networks.
Neural networks were originally inspired by the way human brains
work — individual “neurons” receive “signals” from other neurons and in
turn send “signals” to other “neurons”. Each neuron transforms the
incoming “signals” in some way, and eventually an output signal is
produced. If everything went well that signal represents a correct
prediction!
This
is a helpful mental model, but computers are not biological brains.
They do not have neurons, or synapses, or any of the other biological
mechanisms that make brains work. Because the biological model breaks
down, researchers and scientists instead use graph theory to model
neural networks — instead of describing neural networks as “artificial
brains”, they describe them as complex graphs with powerful properties.
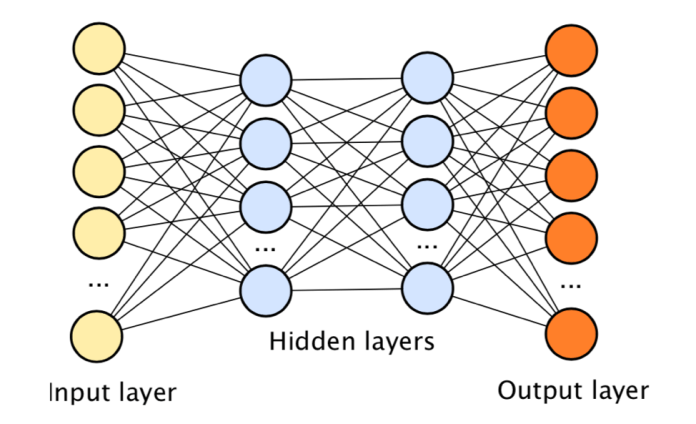
Viewed
through the lens of graph theory a neural network is a series of layers
of connected nodes; each node represents a “neuron” and each connection
represents a “synapse”.
Different kinds of nets have different kinds of connections. The
simplest form of deep learning is a deep neural network. A deep neural
network is a graph with a series of fully connected layers. Every
node in a particular layer has an edge to every node in the next layer;
each of these edges is given a different weight. The whole series of
layers is the “brain”. It turns out, if the weights on all these edges
are set just right these graphs can do some incredible “thinking”.
Ultimately,
the Deep Learning Course will be about how to construct different
versions of these graphs; tune the connection weights until the system
works; and try to make sure our machine does what we think
it’s doing. The mechanics that make Deep Learning work, such as
gradient descent and backpropagation, combine a lot of ideas from
different mathematical disciplines. In order to really understand neural networks we need some math background.
Background Knowledge — A Little Bit Of Everything
Given how easy to use libraries like PyTorch and TensorFlow are, it’s really tempting to say, “you don’t need the math that much.”
But after doing the required reading for the two classes, I’m glad I
have some previous math experience. A subset of topics from linear
algebra, calculus, probability, statistics, and graph theory have
already come up.
Getting
this knowledge at university would entail taking roughly 5 courses.
Calculus 1, 2 and 3; linear algebra; and computer science 101. Luckily,
you don’t need each of those fields in their entirety. Based on what I’ve seen so far, this is what I would recommend studying if you want to get into neural networks yourself:
From linear algebra, you need to know the dot product, matrix multiplication (especially the rules for multiplying matrices with different sizes), and transposes. You
don’t have to be able to do these things quickly by hand, but you
should be comfortable enough to do small examples on a whiteboard or
paper. You should also feel comfortable working with “multidimensional
spaces” — deep learning uses a lot of many dimensional vectors.
I love 3Blue1Brown’s Essence of Linear Algebra
for a refresher or an introduction into linear algebra. Additionally,
compute a few dot products and matrix multiplications by hand (with
small vector/matrix sizes). Although we use graph theory to model neural
networks these graphs are represented in the computer by matrices and
vectors for efficiency reasons. You should be comfortable both thinking
about and programming with vectors and matrices.
From calculus you need to know the derivative, and you ideally should know it pretty well. Neural networks involve simple derivatives, the chain rule, partial derivatives, and the gradient. The derivative is used by neural nets to solve optimization problems,
so you should understand how the derivative can be used to find the
“direction of greatest increase”. A good intuition is probably enough,
but if you solve a couple simple optimization problems using the derivative, you’ll be happy you did. 3Blue1Brown also has an Essence of Calculus series, which is lovely as a more holistic review of calculus.
Gradient
descent and backpropagation both make heavy use of derivatives to fine
tune the networks during training. You don’t have to know how to solve
big complex derivatives with compounding chain and product rules, but
having a feel for partial derivatives with simple equations helps a lot.
From probability and statistics, you should know about common distributions, the idea of metrics, accuracy vs precision,
and hypothesis testing. By far the most common applications of neural
networks are to make predictions or judgements of some kind. Is this a
picture of a dog? Will it rain tomorrow? Should I show Tyler this advertisement, or that one? Statistics and probability will help us assess the accuracy and usefulness of these systems.
It’s
worth noting that the statistics appear more on the applied side; the
graph theory, calculus, and linear algebra all appear on the
implementation side. I think it’s best to understand both, but if you’re
only going to be using a library like TensorFlow and are not interested in implementing these algorithms yourself — it might be wise to focus on the statistics more than the calculus & linear algebra.
Finally,
the graph theory. Honestly, if you can define the terms “vertex”,
“edge” and “edge weight” you’ve probably got enough graph theory under
your belt. Even this “Gentle Introduction” has more information than you need.
In the next article in this series I’ll be examining Deep Neural Networks and how they are constructed. See you then!
This article is produced by Teb’s Lab.
To
learn more about my journey to graduate school, and learn what I’m
learning about machine learning, genetics, and bioinformatics you can:
sign up for the Weekly Lab Report, read The Once and Future Student, become a patron on Patreon, or just follow me here on Medium.
No comments:
Post a Comment