https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/
What are Convolutional Neural Networks and why are they important?
Convolutional Neural Networks (
ConvNets or
CNNs) are a category of
Neural Networks
that have proven very effective in areas such as image recognition and
classification. ConvNets have been successful in identifying faces,
objects and traffic signs apart from powering vision in robots and self
driving cars.
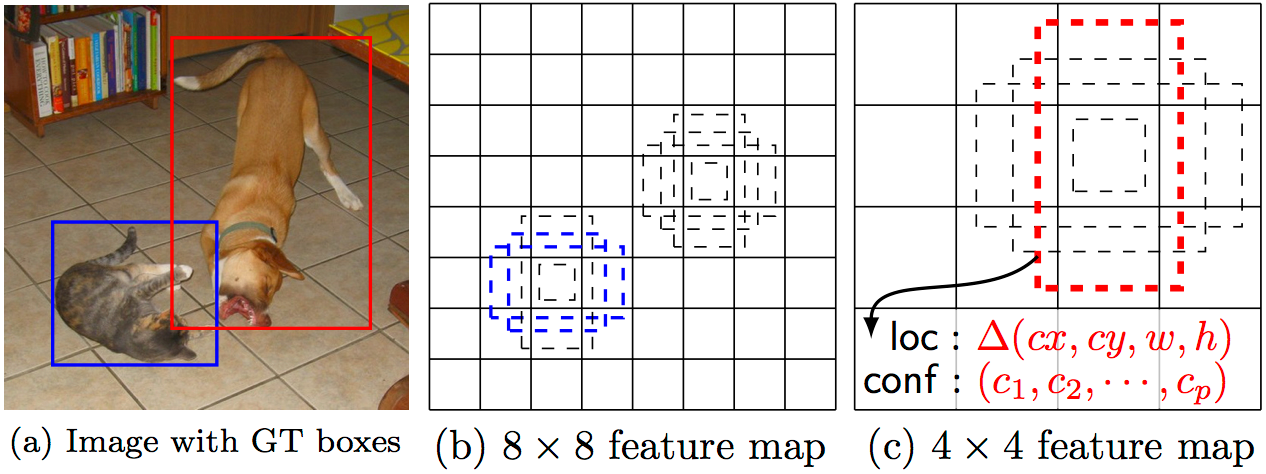
Figure 1: Source [1]
In Figure 1 above, a
ConvNet is able to recognize scenes and the system is able to suggest
relevant captions (“a soccer player is kicking a soccer ball”) while Figure 2
shows an example of ConvNets being used for recognizing everyday
objects, humans and animals. Lately, ConvNets have been effective in
several Natural Language Processing tasks (such as
sentence classification) as well.
Figure 2: Source [2]
ConvNets, therefore, are an important
tool for most machine learning practitioners today. However,
understanding ConvNets and learning to use them for the first time can
sometimes be an intimidating experience. The primary purpose of this
blog post is to develop an understanding of how Convolutional Neural
Networks work on images.
If you are new to neural networks in general, I would recommend reading
this short tutorial on Multi Layer Perceptrons to
get an idea about how they work, before proceeding. Multi Layer
Perceptrons are referred to as “Fully Connected Layers” in this post.
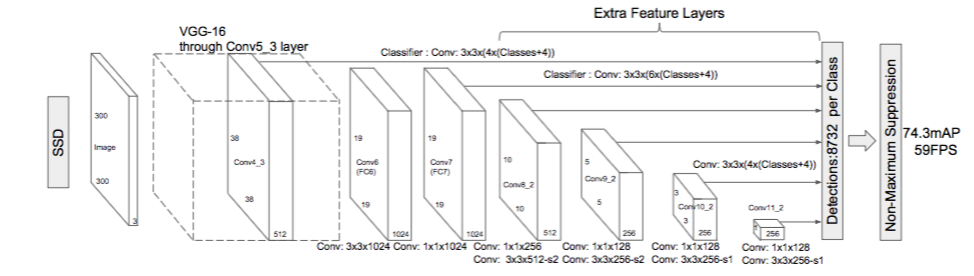
The LeNet Architecture (1990s)
LeNet was one of the very first
convolutional neural networks which helped propel the field of Deep
Learning. This pioneering work by Yann LeCun was named
LeNet5 after many previous successful iterations since the year 1988 [
3]. At that time the LeNet architecture was used mainly for character recognition tasks such as reading zip codes, digits, etc.
Below, we will develop an intuition of
how the LeNet architecture learns to recognize images. There have
been several new architectures proposed in the recent years which are
improvements over the LeNet, but they all use the main concepts from the
LeNet and are relatively easier to understand if you have a clear
understanding of the former.

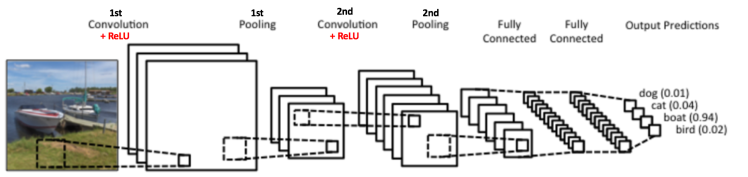
Figure 3: A simple ConvNet. Source [5]
The Convolutional Neural Network in Figure 3 is
similar in architecture to the original LeNet and classifies an input
image into four categories: dog, cat, boat or bird (the original LeNet
was used mainly for character recognition tasks). As evident from the
figure above, on receiving a boat image as input, the network correctly
assigns the highest probability for boat (0.94) among all
four categories. The sum of all probabilities in the output layer should
be one (explained later in this post).
There are four main operations in the ConvNet shown in Figure 3 above:
- Convolution
- Non Linearity (ReLU)
- Pooling or Sub Sampling
- Classification (Fully Connected Layer)
These operations are the basic building blocks of every Convolutional
Neural Network, so understanding how these work is an important step to
developing a sound understanding of ConvNets. We will try to understand
the intuition behind each of these operations below.
An Image is a matrix of pixel values
Essentially, every image can be represented as a matrix of pixel values.
Figure 4: Every image is a matrix of pixel values. Source [6]
Channel
is a conventional term used to refer to a certain component of an
image. An image from a standard digital camera will have three channels
– red, green and blue – you can imagine those as three 2d-matrices
stacked over each other (one for each color), each having pixel values
in the range 0 to 255.
A
grayscale
image, on the other hand, has just one channel. For the purpose of this
post, we will only consider grayscale images, so we will have a single
2d matrix representing an image. The value of each pixel in the matrix
will range from 0 to 255 – zero indicating black and 255 indicating
white.
The Convolution Step
ConvNets derive their name from the
“convolution” operator.
The primary purpose of Convolution in case of a ConvNet is to extract
features from the input image. Convolution preserves the spatial
relationship between pixels by learning image features using small
squares of input data. We will not go into the mathematical details of
Convolution here, but will try to understand how it works over images.
As we discussed above, every image can be
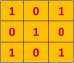
considered as a matrix of pixel values. Consider a 5 x 5 image whose
pixel values are only 0 and 1 (note that for a grayscale image, pixel
values range from 0 to 255, the green matrix below is a special case
where pixel values are only 0 and 1):
Also, consider another 3 x 3 matrix as shown below:
Then, the Convolution of the 5 x 5 image and the 3 x 3 matrix can be computed as shown in the animation in
Figure 5 below:

Figure 5: The Convolution operation. The output matrix is called Convolved Feature or Feature Map. Source [7]
Take a moment to understand how the
computation above is being done. We slide the orange matrix over our
original image (green) by 1 pixel (also called ‘stride’) and for every
position, we compute element wise multiplication (between the two
matrices) and add the multiplication outputs to get the final integer
which forms a single element of the output matrix (pink). Note that the
3×3 matrix “sees” only a part of the input image in each stride.
In CNN terminology, the 3×3 matrix is called a ‘filter‘
or ‘kernel’ or ‘feature detector’ and the matrix formed by sliding the
filter over the image and computing the dot product is called the
‘Convolved Feature’ or ‘Activation Map’ or the ‘Feature Map‘. It is important to note that filters acts as feature detectors from the original input image.
It is evident from the animation above
that different values of the filter matrix will produce different
Feature Maps for the same input image. As an example, consider the
following input image:
In the table below, we can see the
effects of convolution of the above image with different filters. As
shown, we can perform operations such as Edge Detection, Sharpen and
Blur just by changing the numeric values of our filter matrix before the
convolution operation [
8]
– this means that different filters can detect different features from
an image, for example edges, curves etc. More such examples are
available in Section 8.2.4
here.
Another good way to understand the Convolution operation is by looking at the animation in Figure 6 below:
Figure 6: The Convolution Operation. Source [9]
A filter (with red outline) slides over
the input image (convolution operation) to produce a feature map. The
convolution of another filter (with the green outline), over the same
image gives a different feature map as shown. It is important to note
that the Convolution operation captures the local dependencies in the
original image. Also notice how these two different filters
generate different feature maps from the same original image. Remember
that the image and the two filters above are just numeric matrices as we
have discussed above.
In practice, a CNN learns the values of these filters on its own during the training process (although we still need to specify parameters such as number of filters, filter size, architecture of the network
etc. before the training process). The more number of filters we have,
the more image features get extracted and the better our network becomes
at recognizing patterns in unseen images.
The size of the Feature Map (Convolved Feature) is controlled by three parameters [
4] that we need to decide before the convolution step is performed:
- Depth: Depth corresponds to the number of filters we use for the convolution operation. In the network shown in Figure 7,
we are performing convolution of the original boat image using
three distinct filters, thus producing three different feature maps as
shown. You can think of these three feature maps as stacked 2d matrices,
so, the ‘depth’ of the feature map would be three.

Figure 7
- Stride: Stride is the
number of pixels by which we slide our filter matrix over the input
matrix. When the stride is 1 then we move the filters one pixel at a
time. When the stride is 2, then the filters jump 2 pixels at a time as
we slide them around. Having a larger stride will produce smaller
feature maps.
- Zero-padding: Sometimes,
it is convenient to pad the input matrix with zeros around the border,
so that we can apply the filter to bordering elements of our input image
matrix. A nice feature of zero padding is that it allows us to control
the size of the feature maps. Adding zero-padding is also called wide convolution, and not using zero-padding would be a narrow convolution. This has been explained clearly in [14].
Introducing Non Linearity (ReLU)
An additional operation called ReLU has been used after every Convolution operation in Figure 3 above. ReLU stands for Rectified Linear Unit and is a non-linear operation. Its output is given by:
Figure 8: the ReLU operation
ReLU is an element wise operation
(applied per pixel) and replaces all negative pixel values in the
feature map by zero. The purpose of ReLU is to introduce non-linearity
in our ConvNet, since most of the real-world data we would want our
ConvNet to learn would be non-linear (Convolution is a linear operation –
element wise matrix multiplication and addition, so we account for
non-linearity by introducing a non-linear function like ReLU).
The ReLU operation can be understood clearly from Figure 9 below. It shows the ReLU operation applied to one of the feature maps obtained in Figure 6 above. The output feature map here is also referred to as the ‘Rectified’ feature map.

Figure 9: ReLU operation. Source [10]
Other non linear functions such as
tanh or
sigmoid can also be used instead of ReLU, but ReLU has been found to perform better in most situations.
The Pooling Step
Spatial Pooling (also called subsampling
or downsampling) reduces the dimensionality of each feature map but
retains the most important information. Spatial Pooling can be of
different types: Max, Average, Sum etc.
In case of Max Pooling, we define a
spatial neighborhood (for example, a 2×2 window) and take the largest
element from the rectified feature map within that window. Instead of
taking the largest element we could also take the average (Average
Pooling) or sum of all elements in that window. In practice, Max Pooling
has been shown to work better.
Figure 10 shows an
example of Max Pooling operation on a Rectified Feature map (obtained
after convolution + ReLU operation) by using a 2×2 window.
Figure 10: Max Pooling. Source [4]
We slide our 2 x 2 window by 2 cells (also called ‘stride’) and take the maximum value in each region. As shown in Figure 10, this reduces the dimensionality of our feature map.
In the network shown in Figure 11, pooling
operation is applied separately to each feature map (notice that, due
to this, we get three output maps from three input maps).
Figure 11: Pooling applied to Rectified Feature Maps
Figure 12 shows the effect of Pooling on the Rectified Feature Map we received after the ReLU operation in Figure 9 above.
Figure 12: Pooling. Source [10]
The function of Pooling is to progressively reduce the spatial size of the input representation [
4]. In particular, pooling
- makes the input representations (feature dimension) smaller and more manageable
- reduces the number of parameters and computations in the network, therefore, controlling overfitting [4]
- makes the network invariant to small
transformations, distortions and translations in the input image (a
small distortion in input will not change the output of Pooling – since
we take the maximum / average value in a local neighborhood).
- helps us arrive at an almost scale
invariant representation of our image (the exact term is “equivariant”).
This is very powerful since we can detect objects in an image no matter
where they are located (read [18] and [19] for details).
Story so far
Figure 13
So far we have seen how Convolution, ReLU
and Pooling work. It is important to understand that these layers are
the basic building blocks of any CNN. As shown in Figure 13,
we have two sets of Convolution, ReLU & Pooling layers – the 2nd
Convolution layer performs convolution on the output of the first
Pooling Layer using six filters to produce a total of six feature maps.
ReLU is then applied individually on all of these six feature maps. We
then perform Max Pooling operation separately on each of the
six rectified feature maps.
Together these layers extract the useful
features from the images, introduce non-linearity in our network
and reduce feature dimension while aiming to make the features somewhat
equivariant to scale and translation [
18].
The output of the 2nd Pooling Layer acts as an input to the Fully Connected Layer, which we will discuss in the next section.
Fully Connected Layer
The Fully Connected layer is a
traditional Multi Layer Perceptron that uses a softmax activation
function in the output layer (other classifiers like SVM can also be
used, but will stick to softmax in this post). The term “Fully
Connected” implies that every neuron in the previous layer is connected
to every neuron on the next layer. I recommend
reading this post if you are unfamiliar with Multi Layer Perceptrons.
The output from the convolutional and
pooling layers represent high-level features of the input image. The
purpose of the Fully Connected layer is to use these features for
classifying the input image into various classes based on the training
dataset. For example, the image classification task we set out to
perform has four possible outputs as shown in Figure 14 below (note that Figure 14 does not show connections between the nodes in the fully connected layer)
Figure 14: Fully Connected Layer -each node is connected to every other node in the adjacent layer
Apart from classification, adding a
fully-connected layer is also a (usually) cheap way of learning
non-linear combinations of these features. Most of the features from
convolutional and pooling layers may be good for the classification
task, but combinations of those features might be even better [
11].
The sum of output probabilities from the Fully Connected Layer is 1. This is ensured by using the
Softmax
as the activation function in the output layer of the Fully Connected
Layer. The Softmax function takes a vector of arbitrary real-valued
scores and squashes it to a vector of values between zero and one that
sum to one.
Putting it all together – Training using Backpropagation
As discussed above, the Convolution +
Pooling layers act as Feature Extractors from the input image while
Fully Connected layer acts as a classifier.
Note that in Figure 15 below, since the input image is a boat, the target probability is 1 for Boat class and 0 for other three classes, i.e.
- Input Image = Boat
- Target Vector = [0, 0, 1, 0]
Figure 15: Training the ConvNet
The overall training process of the Convolution Network may be summarized as below:
- Step1: We initialize all filters and parameters / weights with random values
- Step2: The
network takes a training image as input, goes through the forward
propagation step (convolution, ReLU and pooling operations along with
forward propagation in the Fully Connected layer) and finds the output
probabilities for each class.
- Lets say the output probabilities for the boat image above are [0.2, 0.4, 0.1, 0.3]
- Since weights are randomly assigned for the first training example, output probabilities are also random.
- Step3: Calculate the total error at the output layer (summation over all 4 classes)
- Total Error = ∑ ½ (target probability – output probability) ²
- Step4: Use Backpropagation to calculate the gradients of the error with respect to all weights in the network and use gradient descent to update all filter values / weights and parameter values to minimize the output error.
- The weights are adjusted in proportion to their contribution to the total error.
- When the same image is input again,
output probabilities might now be [0.1, 0.1, 0.7, 0.1], which is closer
to the target vector [0, 0, 1, 0].
- This means that the network has learnt to classify this particular image correctly by adjusting its weights / filters such that the output error is reduced.
- Parameters like number of filters,
filter sizes, architecture of the network etc. have all been fixed
before Step 1 and do not change during training process – only the
values of the filter matrix and connection weights get updated.
- Step5: Repeat steps 2-4 with all images in the training set.
The above steps train the
ConvNet – this essentially means that all the weights and parameters of
the ConvNet have now been optimized to correctly classify images from
the training set.
When a new (unseen) image is input into
the ConvNet, the network would go through the forward propagation step
and output a probability for each class (for a new image, the output
probabilities are calculated using the weights which have been optimized
to correctly classify all the previous training examples). If our
training set is large enough, the network will (hopefully) generalize
well to new images and classify them into correct categories.
Note 1: The steps above
have been oversimplified and mathematical details have been avoided to
provide intuition into the training process. See [
4] and [
12] for a mathematical formulation and thorough understanding.
Note 2: In the
example above we used two sets of alternating Convolution and Pooling
layers. Please note however, that these operations can be repeated any
number of times in a single ConvNet. In fact, some of the best
performing ConvNets today have tens of Convolution and Pooling layers!
Also, it is not necessary to have a Pooling layer after every
Convolutional Layer. As can be seen in the Figure 16
below, we can have multiple Convolution + ReLU operations in succession
before having a Pooling operation. Also notice how each layer of the
ConvNet is visualized in the Figure 16 below.
Figure 16: Source [4]
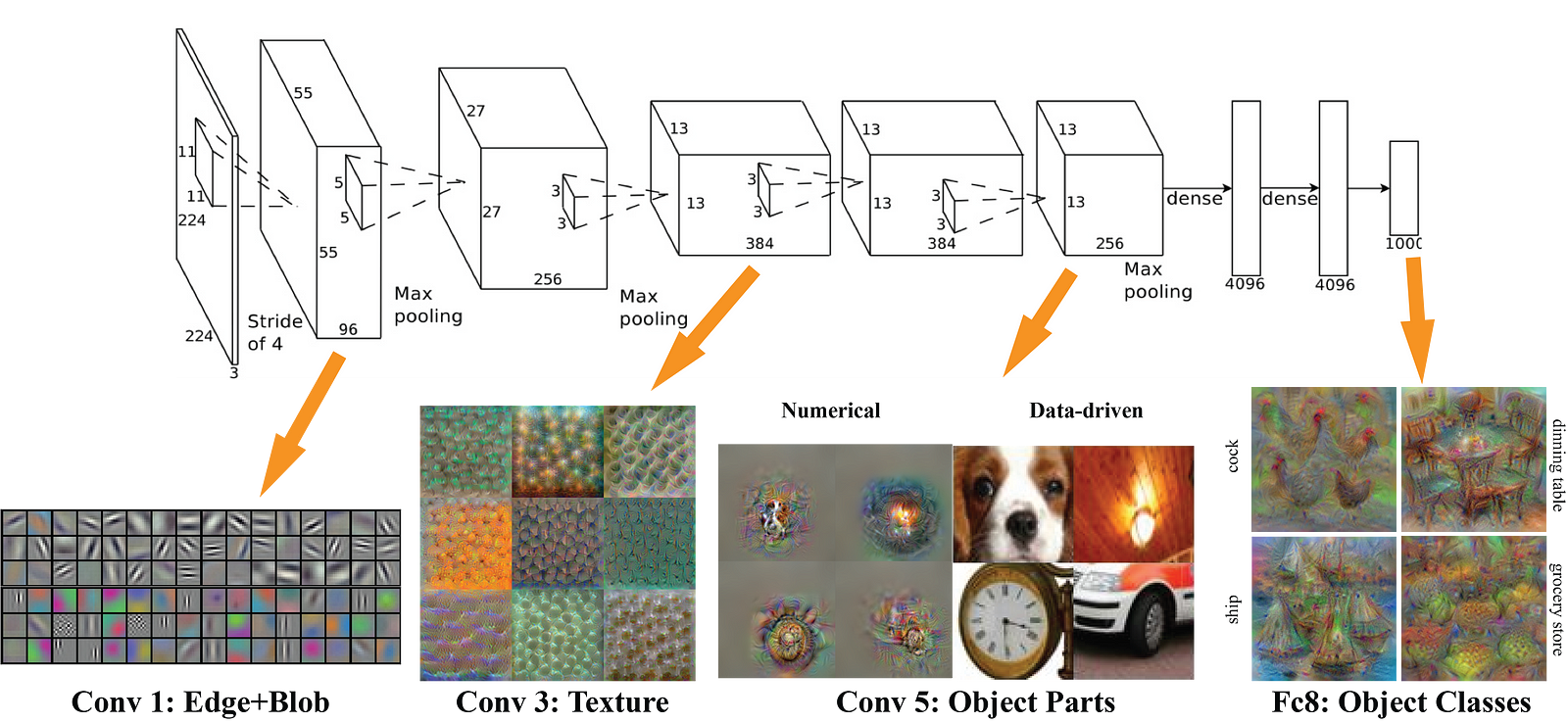
Visualizing Convolutional Neural Networks
In
general, the more convolution steps we have, the more complicated
features our network will be able to learn to recognize. For example, in
Image Classification a ConvNet may learn to detect edges from raw
pixels in the first layer, then use the edges to detect simple shapes in
the second layer, and then use these shapes to deter higher-level
features, such as facial shapes in higher layers [
14]. This is demonstrated in
Figure 17 below – these features were learnt using a
Convolutional Deep Belief Network and
the figure is included here just for demonstrating the idea (this is
only an example: real life convolution filters may detect objects that
have no meaning to humans).
Figure 17: Learned features from a Convolutional Deep Belief Network. Source [21]
Adam Harley created amazing visualizations of a Convolutional Neural Network trained on the MNIST Database of handwritten digits [
13]. I highly recommend
playing around with it to understand details of how a CNN works.
We will see below how the network works for an input ‘8’. Note that the visualization in Figure 18 does not show the ReLU operation separately.
Figure 18: Visualizing a ConvNet trained on handwritten digits. Source [13]
The input image contains 1024 pixels (32 x
32 image) and the first Convolution layer (Convolution Layer 1)
is formed by convolution of six unique 5 × 5 (stride 1) filters with the
input image. As seen, using six different filters produces a
feature map of depth six.
Convolutional Layer 1 is followed by
Pooling Layer 1 that does 2 × 2 max pooling (with stride 2) separately
over the six feature maps in Convolution Layer 1. You can move your
mouse pointer over any pixel in the Pooling Layer and observe the 2 x 2
grid it forms in the previous Convolution Layer (demonstrated in Figure 19). You’ll notice that the pixel having the maximum value (the brightest one) in the 2 x 2 grid makes it to the Pooling layer.
Figure 19: Visualizing the Pooling Operation. Source [13]
Pooling Layer 1 is followed by sixteen 5 ×
5 (stride 1) convolutional filters that perform the convolution
operation. This is followed by Pooling Layer 2 that does 2 × 2 max
pooling (with stride 2). These two layers use the same concepts as
described above.
We then have three fully-connected (FC) layers. There are:
- 120 neurons in the first FC layer
- 100 neurons in the second FC layer
- 10 neurons in the third FC layer corresponding to the 10 digits – also called the Output layer
Notice how in Figure 20,
each of the 10 nodes in the output layer are connected to all 100 nodes
in the 2nd Fully Connected layer (hence the name Fully Connected).
Also, note how the only bright node in
the Output Layer corresponds to ‘8’ – this means that the network
correctly classifies our handwritten digit (brighter node denotes that
the output from it is higher, i.e. 8 has the highest probability among
all other digits).
Figure 20: Visualizing the Filly Connected Layers. Source [13]
The 3d version of the same visualization is available
here.
Other ConvNet Architectures
Convolutional Neural Networks have been around since early 1990s. We discussed the LeNet above which
was one of the very first convolutional neural networks. Some other influential architectures are listed below [
3] [
4].
- LeNet (1990s): Already covered in this article.
- 1990s to 2012: In the years from late 1990s to
early 2010s convolutional neural network were in incubation. As more and
more data and computing power became available, tasks that
convolutional neural networks could tackle became more and more
interesting.
- AlexNet (2012) – In 2012, Alex Krizhevsky (and others) released AlexNet
which was a deeper and much wider version of the LeNet and won by a
large margin the difficult ImageNet Large Scale Visual Recognition
Challenge (ILSVRC) in 2012. It was a significant breakthrough with
respect to the previous approaches and the current widespread
application of CNNs can be attributed to this work.
- ZF Net (2013) – The ILSVRC 2013 winner was a Convolutional Network from Matthew Zeiler and Rob Fergus. It became known as the ZFNet (short for Zeiler & Fergus Net). It was an improvement on AlexNet by tweaking the architecture hyperparameters.
- GoogLeNet (2014) – The ILSVRC 2014 winner was a Convolutional Network from Szegedy et al. from Google. Its main contribution was the development of an Inception Module that dramatically reduced the number of parameters in the network (4M, compared to AlexNet with 60M).
- VGGNet (2014) – The runner-up in ILSVRC 2014 was the network that became known as the VGGNet.
Its main contribution was in showing that the depth of the network
(number of layers) is a critical component for good performance.
- ResNets (2015) – Residual Network
developed by Kaiming He (and others) was the winner of ILSVRC
2015. ResNets are currently by far state of the art Convolutional Neural
Network models and are the default choice for using ConvNets in
practice (as of May 2016).
- DenseNet (August 2016) – Recently published by Gao Huang (and others), the Densely Connected Convolutional Network has
each layer directly connected to every other layer in a feed-forward
fashion. The DenseNet has been shown to obtain significant improvements
over previous state-of-the-art architectures on five highly competitive
object recognition benchmark tasks. Check out the Torch implementation here.
Conclusion
In this post, I have tried to explain the
main concepts behind Convolutional Neural Networks in simple terms.
There are several details I have oversimplified / skipped, but hopefully
this post gave you some intuition around how they work.
This post was originally inspired from
Understanding Convolutional Neural Networks for NLP
by Denny Britz (which I would recommend reading) and a number of
explanations here are based on that post. For a more thorough
understanding of some of these concepts, I would encourage you to go
through the
notes from
Stanford’s course on ConvNets as
well as other excellent resources mentioned under References below. If
you face any issues understanding any of the above concepts or have
questions / suggestions, feel free to leave a comment below.
All images and animations used in this post belong to their respective authors as listed in References section below.
References
- karpathy/neuraltalk2: Efficient Image Captioning code in Torch, Examples
- Shaoqing Ren, et al, “Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks”, 2015, arXiv:1506.01497
- Neural Network Architectures, Eugenio Culurciello’s blog
- CS231n Convolutional Neural Networks for Visual Recognition, Stanford
- Clarifai / Technology
- Machine Learning is Fun! Part 3: Deep Learning and Convolutional Neural Networks
- Feature extraction using convolution, Stanford
- Wikipedia article on Kernel (image processing)
- Deep Learning Methods for Vision, CVPR 2012 Tutorial
- Neural Networks by Rob Fergus, Machine Learning Summer School 2015
- What do the fully connected layers do in CNNs?
- Convolutional Neural Networks, Andrew Gibiansky
- A. W. Harley, “An Interactive Node-Link Visualization of Convolutional Neural Networks,” in ISVC, pages 867-877, 2015 (link). Demo
- Understanding Convolutional Neural Networks for NLP
- Backpropagation in Convolutional Neural Networks
- A Beginner’s Guide To Understanding Convolutional Neural Networks
- Vincent Dumoulin, et al, “A guide to convolution arithmetic for deep learning”, 2015, arXiv:1603.07285
- What is the difference between deep learning and usual machine learning?
- How is a convolutional neural network able to learn invariant features?
- A Taxonomy of Deep Convolutional Neural Nets for Computer Vision
- Honglak Lee, et al, “Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations” (link)