A Beginner's Guide To Understanding Convolutional Neural Networks
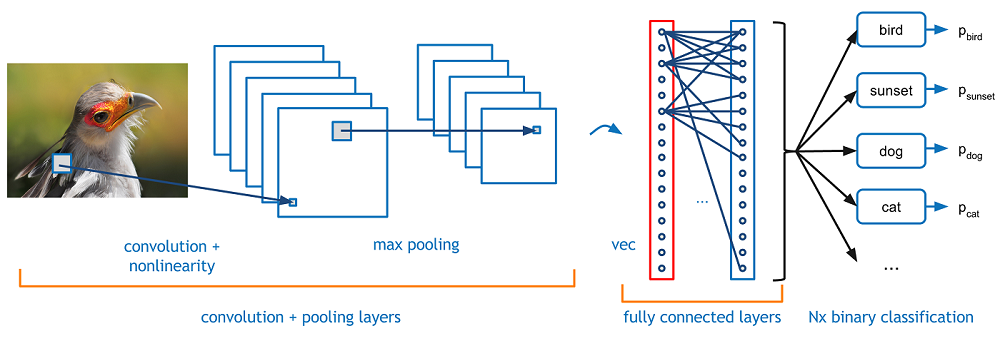
Introduction
Convolutional neural networks. Sounds like a weird combination of biology and math with a little CS sprinkled in, but these networks have been some of the most influential innovations in the field of computer vision. 2012 was the first year that neural nets grew to prominence as Alex Krizhevsky used them to win that year’s ImageNet competition (basically, the annual Olympics of computer vision), dropping the classification error record from 26% to 15%, an astounding improvement at the time.Ever since then, a host of companies have been using deep learning at the core of their services. Facebook uses neural nets for their automatic tagging algorithms, Google for their photo search, Amazon for their product recommendations, Pinterest for their home feed personalization, and Instagram for their search infrastructure.
However, the classic, and arguably most popular, use case of these
networks is for image processing. Within image processing, let’s take a
look at how to use these CNNs for image classification.The Problem Space
Image classification is the task of taking an input image and outputting a class (a cat, dog, etc) or a probability of classes that best describes the image. For humans, this task of recognition is one of the first skills we learn from the moment we are born and is one that comes naturally and effortlessly as adults. Without even thinking twice, we’re able to quickly and seamlessly identify the environment we are in as well as the objects that surround us. When we see an image or just when we look at the world around us, most of the time we are able to immediately characterize the scene and give each object a label, all without even consciously noticing. These skills of being able to quickly recognize patterns, generalize from prior knowledge, and adapt to different image environments are ones that we do not share with our fellow machines.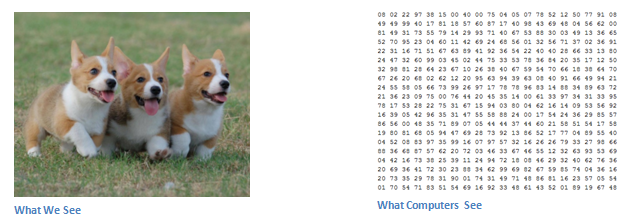
Inputs and Outputs
When a computer sees an image (takes an image as input), it will see an array of pixel values. Depending on the resolution and size of the image, it will see a 32 x 32 x 3 array of numbers (The 3 refers to RGB values). Each of these numbers is given a value from 0 to 255 which describes the pixel intensity at that point. These numbers, while meaningless to us when we perform image classification, are the only inputs available to the computer. The idea is that you give the computer this array of numbers and it will output numbers that describe the probability of the image being a certain class (.80 for cat, .15 for dog, .05 for bird, etc).What We Want the Computer to Do
Now that we know the problem as well as the inputs and outputs, let’s think about how to approach this. What we want the computer to do is to be able to differentiate between all the images it’s given and figure out the unique features that make a dog a dog or that make a cat a cat. This is the process that goes on in our minds subconsciously as well. When we look at a picture of a dog, we can classify it as such if the picture has identifiable features such as paws or 4 legs. In a similar way, the computer is able perform image classification by looking for low level features such as edges and curves, and then building up to more abstract concepts through a series of convolutional layers. This is a general overview of what a CNN does. Let’s get into the specifics.Biological Connection
But first, a little background. When you first heard of the term convolutional neural networks, you may have thought of something related to neuroscience or biology, and you would be right. Sort of. CNNs do take a biological inspiration from the visual cortex. The visual cortex has small regions of cells that are sensitive to specific regions of the visual field. This idea was expanded upon by a fascinating experiment by Hubel and Wiesel in 1962 (Video) where they showed that some individual neuronal cells in the brain responded (or fired) only in the presence of edges of a certain orientation. For example, some neurons fired when exposed to vertical edges and some when shown horizontal or diagonal edges. Hubel and Wiesel found out that all of these neurons were organized in a columnar architecture and that together, they were able to produce visual perception. This idea of specialized components inside of a system having specific tasks (the neuronal cells in the visual cortex looking for specific characteristics) is one that machines use as well, and is the basis behind CNNs.Structure
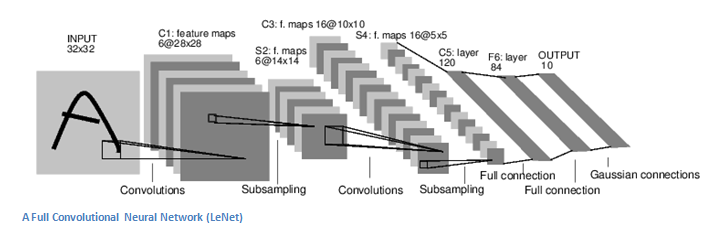
Back to the specifics. A more detailed overview of what CNNs do would be that you take the image, pass it through a series of convolutional, nonlinear, pooling (downsampling), and fully connected layers, and get an output. As we said earlier, the output can be a single class or a probability of classes that best describes the image. Now, the hard part is understanding what each of these layers do. So let’s get into the most important one.First Layer – Math Part
The first layer in a CNN is always a Convolutional Layer. First thing to make sure you remember is what the input to this conv (I’ll be using that abbreviation a lot) layer is. Like we mentioned before, the input is a 32 x 32 x 3 array of pixel values. Now, the best way to explain a conv layer is to imagine a flashlight that is shining over the top left of the image. Let’s say that the light this flashlight shines covers a 5 x 5 area. And now, let’s imagine this flashlight sliding across all the areas of the input image. In machine learning terms, this flashlight is called a filter(or sometimes referred to as a neuron or a kernel) and the region that it is shining over is called the receptive field. Now this filter is also an array of numbers (the numbers are called weights or parameters). A very important note is that the depth of this filter has to be the same as the depth of the input (this makes sure that the math works out), so the dimensions of this filter is 5 x 5 x 3. Now, let’s take the first position the filter is in for example. It would be the top left corner. As the filter is sliding, or convolving, around the input image, it is multiplying the values in the filter with the original pixel values of the image (aka computing dot products). These multiplications are all summed up (mathematically speaking, this would be 75 multiplications in total). So now you have a single number. Remember, this number is just representative of when the filter is at the top left of the image. Now, we repeat this process for every location on the input volume. (Next step would be moving the filter to the right by 1 unit, then right again by 1, and so on). Every unique location on the input volume produces a number. After sliding the filter over all the locations, you will find out that what you’re left with is a 28 x 28 x 1 array of numbers, which we call an activation map or feature map. The reason you get a 28 x 28 array is that there are 784 different locations that a 5 x 5 filter can fit on a 32 x 32 input image. These 784 numbers are mapped to a 28 x 28 array.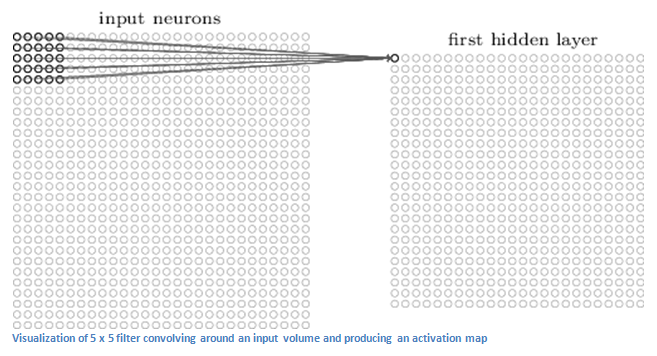
Let’s say now we use two 5 x 5 x 3 filters instead of one. Then our
output volume would be 28 x 28 x 2. By using more filters, we are able
to preserve the spatial dimensions better. Mathematically, this is
what’s going on in a convolutional layer.First Layer – High Level Perspective
However, let’s talk about what this convolution is actually doing from a high level. Each of these filters can be thought of as feature identifiers. When I say features, I’m talking about things like straight edges, simple colors, and curves. Think about the simplest characteristics that all images have in common with each other. Let’s say our first filter is 7 x 7 x 3 and is going to be a curve detector. (In this section, let’s ignore the fact that the filter is 3 units deep and only consider the top depth slice of the filter and the image, for simplicity.)As a curve detector, the filter will have a pixel structure in which there will be higher numerical values along the area that is a shape of a curve (Remember, these filters that we’re talking about as just numbers!).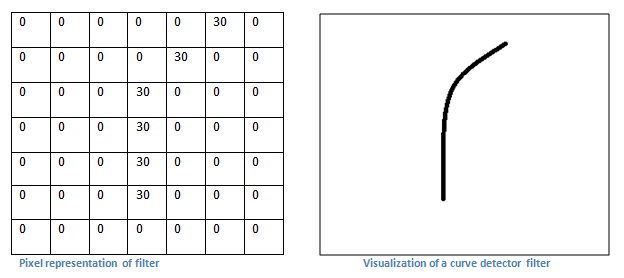
Now, let’s go back to visualizing this
mathematically. When we have this filter at the top left corner of the
input volume, it is computing dot products between the filter and pixel
values at that region. Now let’s take an example of an image that we
want to classify, and let’s put our filter at the top left corner.
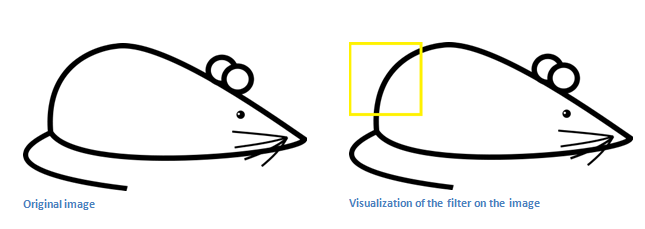
Remember, what we have to do is multiply the values in the filter with the original pixel values of the image.
Basically, in the input image, if there is a shape that generally
resembles the curve that this filter is representing, then all of the
dot products summed together will result in a large value! Now let’s see
what happens when we move our filter.
The value is much lower! This is because
there wasn’t anything in the image section that responded to the curve
detector filter. Remember, the output of this conv layer is an
activation map. So, in the simple case of a one filter convolution (and
if that filter is a curve detector), the activation map will show the
areas in which there at mostly likely to be curves in the picture. In
this example, the top left value of our 28 x 28 x 1 activation map will
be 6600. This high value means that it is likely that there is some sort
of curve in the input volume that caused the filter to activate. The
top right value in our activation map will be 0 because there wasn’t
anything in the input volume that caused the filter to activate (or more
simply said, there wasn’t a curve in that region of the original
image). Remember, this is just for one filter. This is just a filter
that is going to detect lines that curve outward and to the right. We
can have other filters for lines that curve to the left or for straight
edges. The more filters, the greater the depth of the activation map,
and the more information we have about the input volume.
Disclaimer: The filter I
described in this section was simplistic for the main purpose of
describing the math that goes on during a convolution. In the picture
below, you’ll see some examples of actual visualizations of the filters
of the first conv layer of a trained network. Nonetheless, the main
argument remains the same. The filters on the first layer convolve
around the input image and “activate” (or compute high values) when the
specific feature it is looking for is in the input volume.
Going Deeper Through the Network
Now in a traditional
convolutional neural network architecture, there are other layers that
are interspersed between these conv layers. I’d strongly encourage those
interested to read up on them and understand their function and
effects, but in a general sense, they provide nonlinearities and
preservation of dimension that help to improve the robustness of the
network and control overfitting. A classic CNN architecture would look
like this.
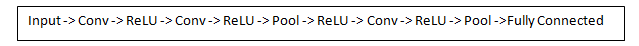
The last layer, however, is an important
one and one that we will go into later on. Let’s just take a step back
and review what we’ve learned so far. We talked about what the filters
in the first conv layer are designed to detect. They detect low level
features such as edges and curves. As one would imagine, in order to
predict whether an image is a type of object, we need the network to be
able to recognize higher level features such as hands or paws or ears.
So let’s think about what the output of the network is after the first
conv layer. It would be a 28 x 28 x 3 volume (assuming we use three 5 x 5
x 3 filters). When we go through another conv layer, the output of the
first conv layer becomes the input of the 2nd conv layer.
Now, this is a little bit harder to visualize. When we were talking
about the first layer, the input was just the original image. However,
when we’re talking about the 2nd conv layer, the input is the
activation map(s) that result from the first layer. So each layer of
the input is basically describing the locations in the original image
for where certain low level features appear. Now when you apply a set of
filters on top of that (pass it through the 2nd conv layer),
the output will be activations that represent higher level features.
Types of these features could be semicircles (combination of a curve and
straight edge) or squares (combination of several straight edges). As
you go through the network and go through more conv layers, you get
activation maps that represent more and more complex features. By the
end of the network, you may have some filters that activate when there
is handwriting in the image, filters that activate when they see pink
objects, etc. If you want more information about visualizing filters in
ConvNets, Matt Zeiler and Rob Fergus had an excellent research paper discussing the topic. Jason Yosinski also has a video
on YouTube that provides a great visual representation. Another
interesting thing to note is that as you go deeper into the network, the
filters begin to have a larger and larger receptive field, which means
that they are able to consider information from a larger area of the
original input volume (another way of putting it is that they are more
responsive to a larger region of pixel space).
Fully Connected Layer
Now that we can detect these high level features, the icing on the cake is attaching a fully connected layer
to the end of the network. This layer basically takes an input volume
(whatever the output is of the conv or ReLU or pool layer preceding it)
and outputs an N dimensional vector where N is the number of classes
that the program has to choose from. For example, if you wanted a digit
classification program, N would be 10 since there are 10 digits. Each
number in this N dimensional vector represents the probability of a
certain class. For example, if the resulting vector for a digit
classification program is [0 .1 .1 .75 0 0 0 0 0 .05], then this
represents a 10% probability that the image is a 1, a 10% probability
that the image is a 2, a 75% probability that the image is a 3, and a 5%
probability that the image is a 9 (Side note: There are other ways that
you can represent the output, but I am just showing the softmax
approach). The way this fully connected layer works is that it looks at
the output of the previous layer (which as we remember should represent
the activation maps of high level features) and determines which
features most correlate to a particular class. For example, if the
program is predicting that some image is a dog, it will have high values
in the activation maps that represent high level features like a paw or
4 legs, etc. Similarly, if the program is predicting that some image is
a bird, it will have high values in the activation maps that represent
high level features like wings or a beak, etc. Basically, a FC layer
looks at what high level features most strongly correlate to a
particular class and has particular weights so that when you compute the
dot product between the weights and the previous layer, you get the
correct probabilities for the different classes.
Training (AKA:What Makes this Stuff Work)
Now, this is the one aspect
of neural networks that I purposely haven’t mentioned yet and it is
probably the most important part. There may be a lot of questions you
had while reading. How do the filters in the first conv layer know to
look for edges and curves? How does the fully connected layer know what
activation maps to look at? How do the filters in each layer know what
values to have? The way the computer is able to adjust its filter values
(or weights) is through a training process called backpropagation.
Before we get into backpropagation, we must
first take a step back and talk about what a neural network needs in
order to work. At the moment we all were born, our minds were fresh. We
didn’t know what a cat or dog or bird was. In a similar sort of way,
before the CNN starts, the weights or filter values are randomized. The
filters don’t know to look for edges and curves. The filters in the
higher layers don’t know to look for paws and beaks. As we grew older
however, our parents and teachers showed us different pictures and
images and gave us a corresponding label. This idea of being given an
image and a label is the training process that CNNs go through. Before
getting too into it, let’s just say that we have a training set that has
thousands of images of dogs, cats, and birds and each of the images has
a label of what animal that picture is. Back to backprop.
So backpropagation can be separated into 4
distinct sections, the forward pass, the loss function, the backward
pass, and the weight update. During the forward pass,
you take a training image which as we remember is a 32 x 32 x 3 array of
numbers and pass it through the whole network. On our first training
example, since all of the weights or filter values were randomly
initialized, the output will probably be something like [.1 .1 .1 .1 .1
.1 .1 .1 .1 .1], basically an output that doesn’t give preference to any
number in particular. The network, with its current weights, isn’t able
to look for those low level features or thus isn’t able to make any
reasonable conclusion about what the classification might be. This goes
to the loss function part of backpropagation. Remember
that what we are using right now is training data. This data has both an
image and a label. Let’s say for example that the first training image
inputted was a 3. The label for the image would be [0 0 0 1 0 0 0 0 0
0]. A loss function can be defined in many different ways but a common
one is MSE (mean squared error), which is ½ times (actual - predicted)
squared.
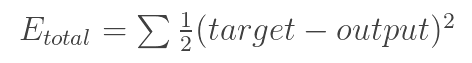
Let’s say the variable L is equal to that
value. As you can imagine, the loss will be extremely high for the first
couple of training images. Now, let’s just think about this
intuitively. We want to get to a point where the predicted label (output
of the ConvNet) is the same as the training label (This means that our
network got its prediction right).In order to get there, we want to
minimize the amount of loss we have. Visualizing this as just an
optimization problem in calculus, we want to find out which inputs
(weights in our case) most directly contributed to the loss (or error)
of the network.
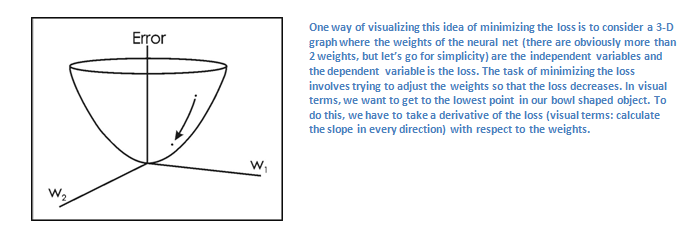
This is the mathematical equivalent of a dL/dW where W are the weights at a particular layer. Now, what we want to do is perform a backward pass
through the network, which is determining which weights contributed
most to the loss and finding ways to adjust them so that the loss
decreases. Once we compute this derivative, we then go to the last step
which is the weight update. This is where we take all the weights of the filters and update them so that they change in the direction of the gradient.
The learning rate is a
parameter that is chosen by the programmer. A high learning rate means
that bigger steps are taken in the weight updates and thus, it may take
less time for the model to converge on an optimal set of weights.
However, a learning rate that is too high could result in jumps that are
too large and not precise enough to reach the optimal point.
The process of forward pass, loss function, backward pass, and parameter update is generally called one epoch.
The program will repeat this process for a fixed number of epochs for
each training image. Once you finish the parameter update on the last
training example, hopefully the network should be trained well enough so
that the weights of the layers are tuned correctly.
Testing
Finally, to see whether or
not our CNN works, we have a different set of images and labels (can’t
double dip between training and test!) and pass the images through the
CNN. We compare the outputs to the ground truth and see if our network
works!
How Companies Use CNNs
Data, data, data. The
companies that have lots of this magic 4 letter word are the ones that
have an inherent advantage over the rest of the competition. The more
training data that you can give to a network, the more training
iterations you can make, the more weight updates you can make, and the
better tuned to the network is when it goes to production. Facebook (and
Instagram) can use all the photos of the billion users it currently
has, Pinterest can use information of the 50 billion pins that are on
its site, Google can use search data, and Amazon can use data from the
millions of products that are bought every day. And now you know the
magic behind how they use it.
Disclaimer
While this post should be a
good start to understanding CNNs, it is by no means a comprehensive
overview. Things not discussed in this post include the nonlinear and
pooling layers as well as hyperparameters of the network such as filter
sizes, stride, and padding. Topics like network architecture, batch
normalization, vanishing gradients, dropout, initialization techniques,
non-convex optimization,biases, choices of loss functions, data
augmentation,regularization methods, computational considerations,
modifications of backpropagation, and more were also not discussed (yet ).
Sources
No comments:
Post a Comment