Convolution is probably the most
important concept in deep learning right now. It was convolution and
convolutional nets that catapulted deep learning to the forefront of
almost any machine learning task there is. But what makes convolution so
powerful? How does it work? In this blog post I will explain
convolution and relate it to other concepts that will help you to
understand convolution thoroughly.
There are already some blog post
regarding convolution in deep learning, but I found all of them highly
confusing with unnecessary mathematical details that do not further the
understanding in any meaningful way. This blog post will also have many
mathematical details, but I will approach them from a conceptual point
of view where I represent the underlying mathematics with images
everybody should be able to understand. The first part of this blog post
is aimed at anybody who wants to understand the general concept of
convolution and convolutional nets in deep learning. The second part of
this blog post includes advanced concepts and is aimed to further and
enhance the understanding of convolution for deep learning researchers
and specialists.
What is convolution?
This whole blog post will build up to
answer exactly this question, but it may be very helpful to first
understand in which direction this is going, so what is convolution in
rough terms?
You can imagine convolution as the mixing
of information. Imagine two buckets full of information which are
poured into one single bucket and then mixed according to a specific
rule. Each bucket of information has its own recipe, which describes how
the information in one bucket mixes with the other. So convolution is
an orderly procedure where two sources of information are intertwined.
Convolution can also be described
mathematically, in fact, it is a mathematical operation like addition,
multiplication or a derivative, and while this operation is
complex in itself, it can be very useful to simplify even more complex
equations. Convolutions are heavily used in physics and engineering to
simplify such complex equations and in the second part — after a short
mathematical development of convolution — we will relate and integrate
ideas between these fields of science and deep learning to gain a
deeper understanding of convolution. But for now we will look at
convolution from a practical perspective.
How do we apply convolution to images?
When we apply convolution to images, we
apply it in two dimensions — that is the width and height of the image.
We mix two buckets of information: The first bucket is the input image,
which has a total of three matrices of pixels — one matrix each for the
red, blue and green color channels; a pixel consists of an integer value
between 0 and 255 in each color channel. The second bucket is the
convolution kernel, a single matrix of floating point numbers where the
pattern and the size of the numbers can be thought of as a recipe for
how to intertwine the input image with the kernel in the convolution
operation. The output of the kernel is the altered image which is often
called a feature map in deep learning. There will be one feature map for
every color channel.
We now perform the actual intertwining of
these two pieces of information through convolution. One way to apply
convolution is to take an image patch from the input image of the size
of the kernel — here we have a 100×100 image, and a 3×3 kernel, so we
would take 3×3 patches — and then do an element wise multiplication with
the image patch and convolution kernel. The sum of this multiplication
then results in one pixel of the feature map. After one pixel
of the feature map has been computed, the center of the image patch
extractor slides one pixel into another direction, and repeats this
computation. The computation ends when all pixels of the feature map
have been computed this way. This procedure is illustrated for one image
patch in the following gif.
As you can see there is also a
normalization procedure where the output value is normalized by the size
of the kernel (9); this is to ensure that the total intensity of the
picture and the feature map stays the same.
Why is convolution of images useful in machine learning?
There can be a lot of distracting
information in images that is not relevant to what we are trying to
achieve. A good example of this is a project I did together with Jannek Thomas in the Burda Bootcamp.
The Burda Bootcamp is a rapid prototyping lab where students work in a
hackathon-style environment to create technologically risky products in
very short intervals. Together with my 9 colleagues,
we created 11 products in 2 months. In one project I wanted to build a
fashion image search with deep autoencoders: You upload an image of a
fashion item and the autoencoder should find images that contain clothes
with similar style.
Now if you want to differentiate between
styles of clothes, the colors of the clothes will not be that useful for
doing that; also minute details like emblems of the brand will be
rather unimportant. What is most important is probably the shape of the
clothes. Generally, the shape of a blouse is very different from the
shape of a shirt, jacket, or trouser. So if we could filter the
unnecessary information out of images then our algorithm will not be
distracted by the unnecessary details like color and branded emblems. We
can achieve this easily by convoluting images with kernels.
My colleague Jannek Thomas preprocessed
the data and applied a Sobel edge detector (similar to the kernel above)
to filter everything out of the image except the outlines of the shape
of an object — this is why the application of convolution is often
called filtering, and the kernels are often called filters (a more exact
definition of this filtering processes will follow below). The
resulting feature map from the edge detector kernel will be very helpful
if you want to differentiate between different types of clothes,
because only relevant shape information remains.
We can take this a step further: There
are dozens of different kernels which produce many different feature
maps, e.g. which sharpen the image (more details), or which blur the
image (less details), and each feature map may help our algorithm to do
better on its task (details, like 3 instead of 2 buttons on your jacket
might be important).
Using this kind of procedure — taking
inputs, transforming inputs and feeding the transformed inputs to an
algorithm — is called feature engineering. Feature engineering is very
difficult, and there are little resources which help you to learn this
skill. In consequence, there are very few people which can apply feature
engineering skillfully to a wide range of tasks. Feature engineering is
— hands down — the most important skill to score well in Kaggle competitions.
Feature engineering is so difficult because for each type of data and
each type of problem, different features do well: Knowledge of feature
engineering for image tasks will be quite useless for time series data;
and even if we have two similar image tasks, it will not be easy to
engineer good features because the objects in the images also determine
what will work and what will not. It takes a lot of experience to get
all of this right.
So feature engineering is very difficult
and you have to start from scratch for each new task in order to do
well. But when we look at images, might it be possible to automatically
find the kernels which are most suitable for a task?
Enter convolutional nets
Convolutional nets do exactly this.
Instead of having fixed numbers in our kernel, we assign parameters to
these kernels which will be trained on the data. As we train our
convolutional net, the kernel will get better and better at filtering a
given image (or a given feature map) for relevant information. This
process is automatic and is called feature learning. Feature learning
automatically generalizes to each new task: We just need to simply train
our network to find new filters which are relevant for the new task.
This is what makes convolutional nets so powerful — no difficulties with
feature engineering!
Usually we do not learn a single kernel
in convolutional nets, instead we learn a hierarchy of multiple kernels
at the same time. For example a 32x16x16 kernel applied to a 256×256
image would produce 32 feature maps of size 241×241 (this is the
standard size, the size may vary from implementation to implementation;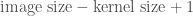 
).
So automatically we learn 32 new features that have relevant
information for our task in them. These feature then provide the inputs
for the next kernel which filters the inputs again. Once we learned our
hierarchical features, we simply pass them to a fully connected, simple
neural network that combines them in order to classify the input image
into classes. That is nearly all that there is to know about
convolutional nets at a conceptual level (pooling procedures are
important too, but that would be another blog post).
).
So automatically we learn 32 new features that have relevant
information for our task in them. These feature then provide the inputs
for the next kernel which filters the inputs again. Once we learned our
hierarchical features, we simply pass them to a fully connected, simple
neural network that combines them in order to classify the input image
into classes. That is nearly all that there is to know about
convolutional nets at a conceptual level (pooling procedures are
important too, but that would be another blog post).Part II: Advanced concepts
We now have a very good intuition of what
convolution is, and what is going on in convolutional nets, and why
convolutional nets are so powerful. But we can dig deeper to understand
what is really going on within a convolution operation. In doing so, we
will see that the original interpretation of computing a convolution is
rather cumbersome and we can develop more sophisticated interpretations
which will help us to think about convolutions much more broadly so that
we can apply them on many different data. To achieve this deeper
understanding the first step is to understand the convolution theorem.
The convolution theorem
To develop the concept of convolution
further, we make use of the convolution theorem, which relates
convolution in the time/space domain — where convolution features an
unwieldy integral or sum — to a mere element wise multiplication in the
frequency/Fourier domain. This theorem is very powerful and is widely
applied in many sciences. The convolution theorem is also one of
the reasons why the fast Fourier transform (FFT) algorithm is thought by
some to be one of the most important algorithms of the 20th century.
The first equation is the one dimensional
continuous convolution theorem of two general continuous functions; the
second equation is the 2D discrete convolution theorem for discrete
image data. Here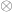 
denotes a convolution operation, 
denotes the Fourier transform, 
the inverse Fourier transform, and 
is a normalization constant. Note that “discrete” here means that our
data consists of a countable number of variables (pixels); and 1D means
that our variables can be laid out in one dimension in a meaningful way,
e.g. time is one dimensional (one second after the other), images are
two dimensional (pixels have rows and columns), videos are three
dimensional (pixels have rows and columns, and images come one after
another).
denotes a convolution operation, denotes the Fourier transform, 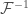the inverse Fourier transform, and
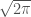is a normalization constant. Note that “discrete” here means that our
data consists of a countable number of variables (pixels); and 1D means
that our variables can be laid out in one dimension in a meaningful way,
e.g. time is one dimensional (one second after the other), images are
two dimensional (pixels have rows and columns), videos are three
dimensional (pixels have rows and columns, and images come one after
another).
To get a better understanding what
happens in the convolution theorem we will now look at the
interpretation of Fourier transforms with respect to digital image
processing.
Fast Fourier transforms
The fast Fourier transform is an
algorithm that transforms data from the space/time domain into the
frequency or Fourier domain. The Fourier transform describes the
original function in a sum of wave-like cosine and sine terms. It is
important to note, that the Fourier transform is generally complex
valued, which means that a real value is transformed into a complex
value with a real and imaginary part. Usually the imaginary part is only
important for certain operations and to transform the frequencies back
into the space/time domain and will be largely ignored in this blog
post. Below you can see a visualization how a signal (a function of
information often with a time parameter, often periodic) is transformed
by a Fourier transform.
You may be unaware of this, but it might
well be that you see Fourier transformed values on a daily basis: If the
red signal is a song then the blue values might be the equalizer bars
displayed by your mp3 player.
The Fourier domain for images
How can we imagine frequencies for
images? Imagine a piece of paper with one of the two patterns from above
on it. Now imagine a wave traveling from one edge of the paper to the
other where the wave pierces through the paper at each stripe of a
certain color and hovers over the other. Such waves pierce the black and
white parts in specific intervals, for example, every two pixels — this
represents the frequency. In the Fourier transform lower frequencies
are closer to the center and higher frequencies are at the edges (the
maximum frequency for an image is at the very edge). The location of
Fourier transform values with high intensity (white in the images) are
ordered according to the direction of the greatest change in intensity
in the original image. This is very apparent from the next image and its
log Fourier transforms (applying the log to the real values decreases
the differences in pixel intensity in the image — we see information
more easily this way).
We immediately see that a Fourier
transform contains a lot of information about the orientation of an
object in an image. If an object is turned by, say, 37% degrees, it is
difficult to tell that from the original pixel information, but very
clear from the Fourier transformed values.
This is an important insight: Due to the
convolution theorem, we can imagine that convolutional nets operate on
images in the Fourier domain and from the images above we now know that
images in that domain contain a lot of information about orientation.
Thus convolutional nets should be better than traditional algorithms
when it comes to rotated images and this is indeed the case (although
convolutional nets are still very bad at this when we compare them to
human vision).
Frequency filtering and convolution
The reason why the convolution operation
is often described as a filtering operation, and why convolution kernels
are often named filters will be apparent from the next example, which
is very close to convolution.
If we transform the original image with a
Fourier transform and then multiply it by a circle padded by zeros
(zeros=black) in the Fourier domain, we filter out all high frequency
values (they will be set to zero, due to the zero padded values). Note
that the filtered image still has the same striped pattern, but its
quality is much worse now — this is how jpeg compression works (although
a different but similar transform is used), we transform the image,
keep only certain frequencies and transform back to the spatial image
domain; the compression ratio would be the size of the black area to the
size of the circle in this example.
If we now imagine that the circle is a
convolution kernel, then we have fully fledged convolution — just as in
convolutional nets. There are still many tricks to speed up and
stabilize the computation of convolutions with Fourier transforms, but
this is the basic principle how it is done.
Now that we have established the meaning
of the convolution theorem and Fourier transforms, we can now apply this
understanding to different fields in science and enhance our
interpretation of convolution in deep learning.
Insights from fluid mechanics
Fluid mechanics concerns itself with the
creation of differential equation models for flows of fluids like air
and water (air flows around an airplane; water flows around suspended
parts of a bridge). Fourier transforms not only simplify convolution,
but also differentiation, and this is why Fourier transforms are widely
used in the field of fluid mechanics, or any field with differential
equations for that matter. Sometimes the only way to find an analytic
solution to a fluid flow problem is to simplify a partial differential
equation with a Fourier transform. In this process we can sometimes
rewrite the solution of such a partial differential equation in terms of
a convolution of two functions which then allows for very easy
interpretation of the solution. This is the case for the diffusion
equation in one dimension, and for some two dimensional diffusion
processes for functions in cylindrical or spherical polar coordinates.
Diffusion
You can mix two fluids (milk and coffee)
by moving the fluid with an outside force (mixing with a spoon) — this
is called convection and is usually very fast. But you could also wait
and the two fluids would mix themselves on their own (if it is
chemically possible) — this is called diffusion and is usually a very
slow when compared to convection.
Imagine an aquarium that is split into
two by a thin, removable barrier where one side of the aquarium is
filled with salt water, and the other side with fresh water. If you now
remove the thin barrier carefully, the two fluids will mix together
until the whole aquarium has the same concentration of salt everywhere.
This process is more “violent” the greater the difference in saltiness
between the fresh water and salt water.
Now imagine you have a square aquarium
with 256×256 thin barriers that separate 256×256 cubes each with
different salt concentration. If you remove the barrier now, there will
be little mixing between two cubes with little difference in salt
concentration, but rapid mixing between two cubes with very different
salt concentrations. Now imagine that the 256×256 grid is an image, the
cubes are pixels, and the salt concentration is the intensity of each
pixel. Instead of diffusion of salt concentrations we now have diffusion
of pixel information.
It turns out, this is exactly one part of
the convolution for the diffusion equation solution: One part is simply
the initial concentrations of a certain fluid in a certain area — or in
image terms — the initial image with its initial pixel intensities. To
complete the interpretation of convolution as a diffusion process we
need to interpret the second part of the solution to the diffusion
equation: The propagator.
Interpreting the propagator
The propagator is a probability density
function, which denotes into which direction fluid particles diffuse
over time. The problem here is that we do not have a probability
function in deep learning, but a convolution kernel — how can we unify
these concepts?
We can apply a normalization that turns
the convolution kernel into a probability density function. This is just
like computing the softmax for output values in a classification tasks.
Here the softmax normalization for the edge detector kernel from the
first example above.
of the kernel and apply 
. After that we divide by the sum of all .
Please note that this technique to calculate the softmax will be fine
for most convolution kernels, but for more complex data the computation
is a bit different to ensure numerical stability (floating point
computation is inherently unstable for very large and very small values
and you have to carefully navigate around troubles in this case).
Now we have a full interpretation of
convolution on images in terms of diffusion. We can imagine the
operation of convolution as a two part diffusion process: Firstly, there
is strong diffusion where pixel intensities change (from black to
white, or from yellow to blue, etc.) and secondly, the diffusion process
in an area is regulated by the probability distribution of the
convolution kernel. That means that each pixel in the kernel area,
diffuses into another position within the kernel according to the kernel
probability density.
For the edge detector above almost all
information in the surrounding area will concentrate in a single space
(this is unnatural for diffusion in fluids, but this interpretation is
mathematically correct). For example all pixels that are under the
0.0001 values, will very likely flow into the center pixel and
accumulate there. The final concentration will be largest where the
largest differences between neighboring pixels are, because here the
diffusion process is most marked. In turn, the greatest differences in
neighboring pixels is there, where the edges between different objects
are, so this explains why the kernel above is an edge detector.
So there we have it: Convolution as
diffusion of information. We can apply this interpretation directly on
other kernels. Sometimes we have to apply a softmax normalization for
interpretation, but generally the numbers in itself say a lot about what
will happen. Take the following kernel for example. Can you now
interpret what that kernel is doing? Click here to find the solution (there is a link back to this position).
Wait, there is something fishy here
How come that we have deterministic
behavior if we have a convolution kernel with probabilities? We have to
interpret that single particles diffuse according to the probability
distribution of the kernel, according to the propagator, don’t we?
Yes, this is indeed true. However, if you
take a tiny piece of fluid, say a tiny drop of water, you still have
millions of water molecules in that tiny drop of water, and while a
single molecule behaves stochastically according to the probability
distribution of the propagator, a whole bunch of molecules have quasi
deterministic behavior —this is an important interpretation from
statistical mechanics and thus also for diffusion in fluid mechanics. We
can interpret the probabilities of the propagator as the average
distribution of information or pixel intensities; Thus our
interpretation is correct from a viewpoint of fluid mechanics. However,
there is also a valid stochastic interpretation for convolution.
Insights from quantum mechanics
The propagator is an important concept in
quantum mechanics. In quantum mechanics a particle can be in a
superposition where it has two or more properties which usually exclude
themselves in our empirical world: For example, in quantum mechanics a
particle can be at two places at the same time — that is a single
object in two places.
However, when you measure the state of
the particle — for example where the particle is right now — it will be
either at one place or the other. In other terms, you destroy the
superposition state by observation of the particle. The propagator then
describes the probability distribution where you can expect the particle
to be. So after measurement a particle might be — according to the
probability distribution of the propagator — with 30% probability in
place A and 70% probability in place B.
If we have entangled particles (spooky
action at a distance), a few particles can hold hundreds or even
millions of different states at the same time — this is the power
promised by quantum computers.
So if we use this interpretation for deep
learning, we can think that the pixels in an image are in a
superposition state, so that in each image patch, each pixel is in 9
positions at the same time (if our kernel is 3×3). Once we apply the
convolution we make a measurement and the superposition of each pixel
collapses into a single position as described by the probability
distribution of the convolution kernel, or in other words: For each
pixel, we choose one pixel of the 9 pixels at random (with the
probability of the kernel) and the resulting pixel is the average of all
these pixels. For this interpretation to be true, this needs to be a
true stochastic process, which means, the same image and the same kernel
will generally yield different results. This interpretation does not
relate one to one to convolution but it might give you ideas how to the
apply convolution in stochastic ways or how to develop quantum
algorithms for convolutional nets. A quantum algorithm would be able to
calculate all possible combinations described by the kernel with one computation and in linear time/qubits with respect to the size of image and kernel.
Insights from probability theory
Convolution is closely related to
cross-correlation. Cross-correlation is an operation which takes a small
piece of information (a few seconds of a song) to filter a large piece
of information (the whole song) for similarity (similar techniques are
used on youtube to automatically tag videos for copyrights
infringements).
denotes cross correlation and 
denotes the complex conjugate of 
.
While cross correlation seems unwieldy,
there is a trick with which we can easily relate it to convolution in
deep learning: For images we can simply turn the search image upside
down to perform cross-correlation through convolution. When we perform
convolution of an image of a person with an upside image of a face, then
the result will be an image with one or multiple bright pixels at the
location where the face was matched with the person.
This example also illustrates padding
with zeros to stabilize the Fourier transform and this is required in
many version of Fourier transforms. There are versions which require
different padding schemes: Some implementation warp the kernel around
itself and require only padding for the kernel, and yet other
implementations perform divide-and-conquer steps and require no padding
at all. I will not expand on this; the literature on Fourier transforms
is vast and there are many tricks to be learned to make it run better —
especially for images.
At lower levels, convolutional nets will
not perform cross correlation, because we know that they perform edge
detection in the very first convolutional layers. But in later layers,
where more abstract features are generated, it is possible that a
convolutional net learns to perform cross-correlation by convolution. It
is imaginable that the bright pixels from the cross-correlation will be
redirected to units which detect faces (the Google brain project has
some units in its architecture which are dedicated to faces, cats etc.;
maybe cross correlation plays a role here?).
Insights from statistics
What is the difference between
statistical models and machine learning models? Statistical models often
concentrate on very few variables which can be easily interpreted.
Statistical models are built to answer questions: Is drug A better than
drug B?
Machine learning models are about
predictive performance: Drug A increases successful outcomes by 17.83%
with respect to drug B for people with age X, but 22.34% for people with
age Y.
Machine learning models are often much
more powerful for prediction than statistical models, but they are not
reliable. Statistical models are important to reach accurate and
reliable conclusions: Even when drug A is 17.83% better than drug B, we
do not know if this might be due to chance or not; we need statistical
models to determine this.
Two important statistical models for time
series data are the weighted moving average and the autoregressive
models which can be combined into the ARIMA model (autoregressive
integrated moving average model). ARIMA models are rather weak when
compared to models like long short-term recurrent neural networks, but
ARIMA models are extremely robust when you have low dimensional data
(1-5 dimensions). Although their interpretation is often effortful,
ARIMA models are not a blackbox like deep learning algorithms and this
is a great advantage if you need very reliable models.
It turns out that we can rewrite these
models as convolutions and thus we can show that convolutions in deep
learning can be interpreted as functions which produce local ARIMA
features which are then passed to the next layer. This idea however,
does not overlap fully, and so we must be cautious and see when we
really can apply this idea.
Here 
is a constant function which takes the kernel as parameter; white noise
is data with mean zero, a standard deviation of one, and each
variable is uncorrelated with respect to the other variables.
is a constant function which takes the kernel as parameter; white noise
is data with mean zero, a standard deviation of one, and each
variable is uncorrelated with respect to the other variables.
When we pre-process data we make it often
very similar to white noise: We often center it around zero and set the
variance/standard deviation to one. Creating uncorrelated variables is
less often used because it is computationally intensive, however,
conceptually it is straight forward: We reorient the axes along the
eigenvectors of the data.
Now, if we take
to be the bias, then we have an expression that is very similar to a
convolution in deep learning. So the outputs from a convolutional layer
can be interpreted as outputs from an autoregressive model if we
pre-process the data to be white noise.
to be the bias, then we have an expression that is very similar to a
convolution in deep learning. So the outputs from a convolutional layer
can be interpreted as outputs from an autoregressive model if we
pre-process the data to be white noise.
The interpretation of the weighted moving
average is simple: It is just standard convolution on some data (input)
with a certain weight (kernel). This interpretation becomes clearer
when we look at the Gaussian smoothing kernel at the end of the page.
The Gaussian smoothing kernel can be interpreted as a weighted average
of the pixels in each pixel’s neighborhood, or in other words, the
pixels are averaged in their neighborhood (pixels “blend in”, edges are
smoothed).
While a single kernel cannot create both,
autoregressive and weighted moving average features, we usually have
multiple kernels and in combination all these kernels might contain some
features which are like a weighted moving average model and some
which are like an autoregressive model.
Conclusion
In this blog post we have seen what
convolution is all about and why it is so powerful in deep learning. The
interpretation of image patches is easy to understand and easy to
compute but it has many conceptual limitations. We developed
convolutions by Fourier transforms and saw that Fourier transforms
contain a lot of information about orientation of an image. With
the powerful convolution theorem we then developed an interpretation of
convolution as the diffusion of information across pixels. We then
extended the concept of the propagator in the view of quantum mechanics
to receive a stochastic interpretation of the usually deterministic
process. We showed that cross-correlation is very similar to convolution
and that the performance of convolutional nets may depend on the
correlation between feature maps which is induced through convolution.
Finally, we finished with relating convolution to autoregressive and
moving average models.
Personally, I found it very interesting
to work on this blog post. I felt for long time that my undergraduate
studies in mathematics and statistics were wasted somehow, because they
were so unpractical (even though I study applied math). But
later — like an emergent property — all these thoughts linked together
and practically useful understanding emerged. I think this is a great
example why one should be patient and carefully study all university
courses — even if they seem useless at first.
R. B. Fisher, K. Koryllos, “Interactive Textbooks; Embedding Image Processing Operator Demonstrations in Text”, Int. J. of Pattern Recognition and Artificial Intelligence, Vol 12, No 8, pp 1095-1123, 1998.
Available from 
This leading textbook provides a comprehensive
introduction to the fields of pattern recognition and machine learning.
It is aimed at advanced undergraduates or first-year PhD students, as
well as researchers and practitioners. No previous knowledge of pattern
recognition or machine learning concepts is assumed. This is the first
machine learning textbook to include a comprehensive coverage of recent
developments such as probabilistic graphical models and deterministic
inference methods, and to emphasize a modern Bayesian perspective. It is
suitable for courses on machine learning, statistics, computer science,
signal processing, computer vision, data mining, and bioinformatics.
This hard cover book has 738 pages in full colour, and there are 431
graded exercises (with solutions available below). Extensive support is
provided for course instructors.
